Тип урока: изучение нового материала.
Задачи урока:
- Образовательные:
К концу урока учащиеся должны:
- знать
- понятие баллистического движения;
- особенности баллистического движения;
- график баллистического движения;
- закон баллистического движения
- уметь:
- описывать, объяснять наблюдения и фундаментальные опыты, оказавшие существенное влияние на развитие физики;
- иллюстрировать роль физики в создании важнейших технических объектов.
- Развивающие:
Способствовать развитию
- речи;
- интеллектуальных и творческих способностей в процессе приобретения знаний и умений по физике с использованием современных информационных технологий.
- Воспитательные:
Способствовать формированию:
- познавательного интереса к предмету;
- мировоззрения учащихся.
Техническое оснащение урока:
- Компьютерный класс;
- Мультимедийный проектор, экран;
- Программное обеспечение:
- учебное электронное издание «Открытая физика. Версия 2.6.» Часть 1 – раздел механика.
Лабораторная работа
«Движение тела, брошенного под углом к горизонту».
Создание настроя учащихся
Слово учителя: В многочисленных войнах на протяжении всей истории человечества, враждующие стороны, доказывая свое превосходство, использовали сначала камни, копья и стрелы, а затем и ядра, снаряды
и бомбы.
Успех сражения во многом определялся точностью попадания в цель. При этом точный бросок камня, поражение противника летящим копьем или стрелой фиксировалось воином визуально. Это позволяло (при соответствующей тренировке) повторять свой успех в следующем сражении.
Значительно возросшая с развитием техники скорость и соответственно дальность полета снарядов и пуль сделали возможными дистанционные сражения. Однако разрешающей способности глаза было недостаточно для точного попадания в цель.
До XVI века артиллеристы пользовались таблицами, в которых на основе практических наблюдений были указаны углы, ветер, дальность полета, но меткость попадания была очень низкой. Возникла проблема научного предсказания - как достигнуть высокой меткости попадания снаряда.
Впервые разрешить эту проблему удалось великому астроному и физику Галилео Галилею, исследования которого стимулировали появление баллистики (от греческого слова ballo - бросаю). Баллистика - раздел механики, изучающий движение тел в поле силы тяжести Земли.
Изучение нового материала
Итак, как вы уже, наверное, догадались, тема нашего урока: «Баллистическое движение», цель: изучить баллистическое движение, исследуя экспериментально его особенности.
Заслугой Галилео Галилея стало то, что он впервые предложил рассматривать баллистическое движение как сумму простых, в частности, он предложил данное движение представить как результат сложения двух прямолинейных движений: равномерного движения по оси Ох и равнопеременного движения по оси Оу.
Для описания баллистического движения в качестве первого приближения удобнее всего ввести идеализированную компьютерную модель, в данном случае модель «Движение тела, брошенного под углом к горизонту» на компьютере.
В условиях данной модели тело будем рассматривать как материальную точку, движущуюся с постоянным ускорением свободного падения, при этом пренебрегая изменением высоты подъема тела, сопротивлением воздуха, кривизной поверхности Земли, ее вращением вокруг собственной оси.
Это приближение существенно облегчает расчет траектории тел. Однако такое рассмотрение имеет определенные границы применимости. Например, при полете межконтинентальной баллистической ракеты нельзя пренебрегать кривизной поверхности Земли. При свободном падении тел нельзя не учитывать сопротивление воздуха. Но для достижения поставленной цели в условиях данной модели мы можем пренебречь вышеуказанными величинами.
Итак, посмотрим внимательно на модель. Какие параметры мы имеем возможность изменять?
Ответ учащихся: Модель позволяет изменять:
- во-первых, начальную скорость;
- во-вторых, начальную высоту;
- в-третьих, угол направления движения тела.
Слово учителя: Верно. С помощью данной модели мы постараемся решить экспериментально первую задачу, которую ставил перед собой Галилео Галилей, т. е. попытаемся выяснить, какова форма траектории баллистического движения. Для этого зададим первоначальные значения параметров модели: скорость, равную 25 м/с; угол, равный 300. Выберем точку вылета снаряда в начале отсчета, для этого выставим значение высоты равное нулю. Теперь посмотрим эксперимент. Что представляет собой траектория баллистического движения?
Ответ учащихся: Траекторией баллистического движения является парабола.
Слово учителя:правильно! Но можем ли мы сделать окончательный вывод о том, что форма баллистической траектории является парабола?
Ответ учащихся: Нет. Необходимо проверить правильность высказанной Галилеем гипотезы, произведя несколько экспериментов, изменяя каждый раз параметры модели.
Слово учителя: Хорошо! Давайте вначале изменим угол направления движения снаряда. Для этого изменим, данный параметр на модели, т. е. вместо 300, выставим 200. А остальные величины оставим неизмененными. Рассмотрим эксперимент. Изменилась ли форма траектории баллистического движения?
Ответ учащихся: Нет, форма траектории осталась прежней.
Слово учителя: Теперь попробуем увеличить значение угла до 400,оставив остальные параметры. Посмотрим, что происходит с формой траектории?
(Ставит эксперимент.)
Ответ учащихся: Форма траектории остается прежней.
Слово учителя: Давайте посмотрим, измениться ли ее форма, если мы будем уменьшать или увеличивать другие параметры модели. Например, увеличим скорость движения снаряда до 40 м/с, оставив угол и высоту прежними, и пронаблюдаем за движением снаряда. Изменилась ли траектория баллистического движения?
Ответ учащихся: Нет. Форма траектории не меняется.
Слово учителя: А сейчас уменьшим значение скорости движения до 15 м/с, оставив значение угла и высоты прежними. Пронаблюдаем, изменится ли при этом форма траектории?
Ответ учащихся: Форма траектории не изменяется.
Слово учителя: Как вы думаете, изменится ли форма траектории, если мы будем уменьшать либо увеличивать значение высоты подъема тела?
Ответ учащихся: Наверное, форма траектории останется прежней.
Слово учителя: Проверим это с помощью компьютерного эксперимента. Для этого изменим, значение высоты подъема снаряда до 15м. Внимательно проследим за траекторией движения снаряда. Какова ее форма?
Ответ учащихся: Форма траектории по-прежнему - парабола.
Слово учителя: Итак, можем ли мы на основе всех проделанных опытов сделать окончательный вывод об изменении формы траектории баллистического движения?
Ответ учащихся: Изменив все параметры, мы доказали экспериментально, что при любых значениях угла, высоты, скорости движения снаряда форма траектории остается неизменной.
Слово учителя: Таким образом, первая задача нами решена. Гипотеза Галилео Галилея оказалась верной - формой траектории баллистического движения является парабола. Но Галилей также предложил баллистическое движение рассматривать как результат сложения двух прямолинейных движений: равномерного по оси Ох и равнопеременного по оси ау.
Поэтому второй нашей с вами задачей будет: доказать экспериментально справедливость гипотезы Галилея, т. е. убедится в том, что движение по оси Ох является действительно равномерным. Если движение является равномерным, то какой, по вашему мнению, параметр должен оставаться неизменным?
Ответ учащихся: Скорость, так как равномерное движение - это движение с постоянной скоростью.
Слово учителя: Верно! Это означает, что проекция скорости на ось Ох Uх останется неизменной. Итак, исследуем движение снаряда, выпущеного из начала координат (т. е. высота равна нулю) в режиме «Стробоскоп»,
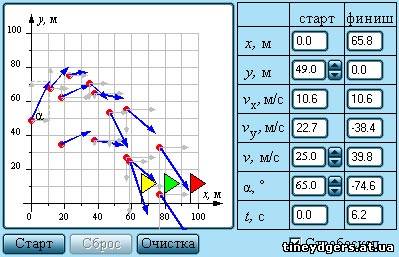
имеющимся на модели, так как именно в этом режиме на траектории через равные промежутки времени указывается направление вектора скорости выпущенного снаряда и его проекции на горизонтальную и вертикальную оси: Uх, Uу. Зададим скорость, равную 25 м/с. Какие параметры мы должны изменять, проводя экспериментальное доказательство?
Ответ учащихся: Мы должны менять угол и высоту.
Слово учителя: Хорошо! Зададим угол движения снаряда, равный 450, а значение высоты, равное нулю. Пронаблюдаем за проекцией скорости на ось Ох - Uх. Что с ней происходит во время движения?
Ответ учащихся: Она останется постоянной.
Слово учителя: То есть движение по оси Ох в данном случае является равномерным. Уменьшим значение угла вылета снаряда до 150. Является ли теперь движение по оси Ох равномерным при условии, что высота подъема останется прежней?
Ответ учащихся: Да. Движение по оси Ох по-прежнему является равномерным.
Слово учителя: Увеличим высоты подъема тела до 20 м, а угол оставим прежним. Какое движение совершает тело по оси Ох?
Ответ учащихся: Снаряд совершает равномерное движение по оси Ох.
Слово учителя: Итак, мы попробовали изменить все параметры, но при этом мы задали лишь один модуль скорости, равный 25 м/с. Попробуем проделать вышеописанные действия, задав другое значение модуля скорости, например, равное 10 м/с (рассуждения проводятся по аналогии, как при значении υ= 25 м/с).
Какой вывод можно сделать о характере движения вдоль оси Ох, пронаблюдав несколько экспериментов, изменяя каждый раз значения параметров модели?
Ответ учащихся: Экспериментально мы доказали верность гипотезы Галилея о том, что движение тела вдоль оси Ох является равномерным.
Слово учителя: Верно! Тем самым мы решили вторую познавательную задачу. Третья задача заключается в доказательстве справедливости гипотезы, высказанной Галилеем, о том, что движение вдоль оси Оу является равнопеременным. Какие параметры мы должны изменять в данном случае?
Ответ учащихся: Мы будем изменять угол, высоту и скорость движения снаряда.
Слово учителя: Хорошо! Тогда зададим первоначальные значения: угла равное 150, высоты - равной 10 м и скорости - равной 20 м/с. Пронаблюдаем, что происходит со значением скорости и величиной вектора скорости движения снаряда? Для этого один из ребят в классе поможет мне зафиксировать значения проекции вектора скорости на ось Оу - υу через равные промежутки времени, например, через каждые 0,5 секунд.
(Проводят опыт, фиксируя значения на доске.)
| t, с |
0 |
0,5 |
1,0 |
1,5 |
2,0 |
2,5 |
3,0 |
3,5 |
4,0 |
|
Uу, м/с |
|
|
|
|
|
|
|
|
|
Слово учителя: Сравним эти значения между собой, для этого найдем разницу: из U2 вычтем U1, из U3 вычтем сумму U2 + U1 и т. д. Что мы видим, сравнив значения проекции скорости на ось Оу через равные промежутки времени?
Ответ учащихся: Эти значения равны между собой.
Слово учителя: Правильно. А сейчас еще раз внимательно посмотрите эксперимент и ответьте на вопрос: как изменяется вертикальная составляющая вектора скорости υу до точки, показывающей максимальную высоту подъема тела, и после того, как тело прошло через эту точку?
Ответ учащихся: Вначале движения до точки hмах, значение проекции скорости на ось Оу - Uу уменьшается до нуля, затем увеличивается до тех пор, пока тело не упадет на землю.
Слово учителя: Итак, мы убедились в том, что в результате баллистического движения, значение проекции вектора скорости на ось Оу изменяется через равные промежутки времени на одинаковую величину. Таким образом, мы можем сделать вывод, что движение тела вдоль оси Оу является равнопеременным. Но можем ли мы считать сформулированный нами вывод окончательным?
Ответ учащихся: Нет. Необходимо проверить правильность высказанной Галилеем гипотезы, произведя несколько исследований, изменяя каждый раз параметры модели.
Слово учителя: Давайте увеличим угол вылета снаряда до 300, а остальные параметры оставим прежними. Посмотрим, что будет происходить с величиной вектора скорости?
(Проводятся аналогичные рассуждения и подсчеты, приведенные выше и учащимся предлагается сделать вывод.)
Ответ учащихся: Величина вектора скорости изменяется за равные промежутки времени на одинаковую величину.
Слово учителя: Что можно сказать о движении тела вдоль оси Оу? Какое оно? Уменьшим угол вылета снаряда до 100, изменится ли характер движения?
(Проводятся аналогичные рассуждения и подсчеты, приведенные выше и учащимся предлагается сделать вывод.)
Ответ учащихся:нет. Движение вдоль оси Оу по-прежнему является равнопеременным.
Слово учителя: Попробуем изменить значение скорости движения снаряда, увеличим ее до 30 м/с. Движение вдоль оси Оу попрежнему остается равнопеременным?
(Проводятся аналогичные рассуждения и подсчеты, приведенные выше и учащимся предлагается сделать вывод.)
Ответ учащихся: Да. Характер движения не изменяется.
Слово учителя: А если мы изменим высоту подъема тела, увеличив ее до 15 м, каким сейчас будет его движение вдоль оси Оу?
(Проводятся аналогичные рассуждения и подсчеты, приведенные выше и учащимся предлагается сделать вывод.)
Ответ учащихся: Движение вдоль оси Оу остается равнопеременным.
Слово учителя: Выставим значение высоты подъема тела, равное нулю. Пронаблюдаем, как будет двигаться снаряд вдоль оси Оу в данном случае?
(Проводятся аналогичные рассуждения и подсчеты, приведенные выше и учащимся предлагается сделать вывод.)
Ответ учащихся: Снаряд будет двигаться равнопеременно.
Слово учителя: Изменяя все параметры, убедились ли мы в справедливости гипотезы Галилео Галилея?
Ответ учащихся: Да, мы убедились в справедливости высказанной Галилеем гипотезы и доказали экспериментально, что движение тела вдоль оси Оу, в условиях баллистического движения является равнопеременным.
Слово учителя: Движение тела, брошенного под углом к горизонту характеризуется временем полета, дальностью полета и высотой подъема. Предлагаю вам получить формулы для расчета основных величин. Пояснения для учащихся:
-
для кинематического описания движения тела удобно одну из осей системы координат (ось OY) направить вертикально вверх, а другую (ось OX) – расположить горизонтально. Тогда движение тела по криволинейной траектории, как мы уже выяснили, можно представить как сумму двух движений, протекающих независимо друг от друга – движения с ускорением свободного падения вдоль оси OY и равномерного прямолинейного движения вдоль оси OX. На рисунке изображен вектор начальной скорости  тела и его проекции на координатные оси. тела и его проекции на координатные оси.
-
-
- так как ускорение свободного падения с течение времени не меняется, то движение тела, как и любое движение с постоянным ускорением, будет описываться уравнениями:
х = х0 + υ0хt + ах t2/2
у = у0 + υ0уt + ау t2/2
- для движения вдоль оси OX имеем следующие условия:
x0 = 0, υ0x = υ0 cos α, ax = 0
а для движения вдоль оси OY
y0 = 0, υ0y = υ0 sin α, ay = – g
- tполета = 2tподъема на мах высоту
(Далее учащиеся работают в группах (4 человека) по выводу формул для расчета времени полета, дальности полета, высоты подъема. Учитель оказывает посильную помощь). Затем осуществляется проверка полученных результатов.
Слово учителя: Но хочу вам напомнить, что все полученные нами результаты справедливы лишь для идеализированной модели, когда можно пренебречь сопротивлением воздуха. Реальное движение тел в земной атмосфере происходит по баллистической траектории, существенно отличающейся от параболической из-за сопротивления воздуха. Чем больше скорость тела, тем больше сила сопротивления воздуха и тем существенней отличие баллистической траектории от параболы. При движении снарядов и пуль в воздухе максимальная дальность полета достигается при угле вылета 300 - 400. Расхождение простейшей теории баллистики с экспериментом не означает, что она не верна в принципе. В вакууме или на Луне, где практически нет атмосферы, эта теория дает правильные результаты. При описании движения тел в атмосфере учет сопротивления воздуха требует математического расчета, которых мы не будем приводить из-за громоздкости. Отметим лишь, что расчет баллистической траектории запуска и выведения на требуемую орбиту спутников Земли и их посадки в заданном районе осуществляют с большой точностью мощные компьютерные станции.
Первичная проверка усвоения знаний
Фронтальный опрос
ВОПРОСЫ
- Что изучает баллистика?
- Какая идеализированная модель используется для описания баллистического движения?
- Каков характер движения тела при баллистическом движении по горизонтали?
- Каков характер движения тела при баллистическом движении по вертикали?
- Что является баллистической траекторией?
Отработка практических умений решать задачи
(работа в парах за компьютером)
Слово учителя: Ребята, предлагаю вам решить задачи, правильность решения которых вы проверите с помощью виртуального эксперимента.
Группа I. Стрела, выпущенная из лука вертикально вверх, упала на землю через 6 с. Какова начальная скорость стрелы и максимальная высота подъёма?
Группа II. Мальчик бросил горизонтально мяч из окна, находящегося на высоте 20 м. Сколько времени летел мяч до земли и с какой скоростью он был брошен, если он упал на расстоянии 6 м от основания дома?
Группа III. Во сколько раз надо увеличить начальную скорость брошенного вверх тела, чтобы высота подъёма увеличилась в 4 раза?
Группа IV. Как изменится время и дальность полёта тела, брошенного горизонтально с некоторой высоты, если скорость бросания увеличить вдвое?
Группа V. Вратарь, выбивая мяч от ворот (с земли), сообщает ему скорость 20 м/с, направленную под углом 500 к горизонту. Найти время полёта мяча, максимальную высоту поднятия и горизонтальную дальность полёта.
Группа VI. С балкона, расположенного на высоте 20 м, бросили мяч под углом 300 вверх от горизонта со скоростью 10 м/с. Найти: а) координату мяча через 2 с; б) через какой промежуток времени мяч упадёт на землю; в) горизонтальную дальность полёта.
Информация о домашнем задании
ДЛЯ ВСЕХ
- Стр. 63 – 70 учебника В.А. Касьянова «Физика -10» - ответить на вопросы стр. 71.
- Получить уравнение траектории у = у (х) движения тела, брошенного под углом к горизонту.
НА ВЫБОР
Установите, при каком значении угла бросания дальность полета максимальна.
ИЛИ
Постройте графики зависимости от времени горизонтальной υх и вертикальной υу проекций скорости тела, брошенного под углом к горизонту.
Рефлексия
Сегодня на уроке мы изучали новую тему, используя возможности компьютера.
- Ваше мнение об уроке: …
- Сегодня я узнал(а)…понял(а)…удивился(ась)…
- Эта тема для понимания…
| 
