Цель урока: формирование умений применять полученные знания при решении типичных и нестандартных задач; повторить, обобщить и применить знание прямой и обратной пропорциональности при решении качественных, расчётных и экспериментальных задач по физике; развивать умение самостоятельно анализировать свою работу; развивать познавательную активность и творческие способности.

Ход урока

I. Организационный этап

II. Устное повторение узловых вопросов алгебры

• Индивидуальная работа у доски:

– Напишите область определения функций:

y₁ = 2x + 1; y₂ = –1/2 · х; y₃ = 2/x.

– Начертите эскиз данных графиков.

– Назовите данную функцию.

• Фронтальная работа с классом:

Что называется функцией? Что называется областью определения функции? Сформулируйте определение линейной функции. Что называется областью определения линейной функции? Что является графиком линейной функции? Сформулируйте определение функции прямой пропорциональности. Что является областью определения этой функции? Что является графиком данной функции? Дайте определение функции обратной пропорциональности. Какова её область определения? Что является графиком данной функции? Назовите эту функцию y = x². Что является областью определения и графиком данной функции?

Из предложенных на доске эскизов графиков различных функций выберите графики линейных функций. В чём их различия?

Укажите графики функции прямой пропорциональности. В чём их различия?

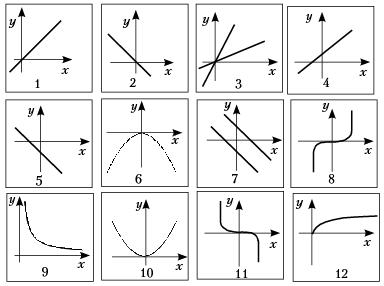
Укажите графики функций обратной пропорциональности.

Графики каких функций мы не назвали?

III. Случаи прямо пропорциональной зависимости в физике

Математика – наука прикладная. Сейчас мы рассмотрим применение прямой и обратной пропорциональности на уроках физики:

• Фронтальная работа с классом:

– Сформулируйте закон Ома для участка цепи.

– Запишите закон на доске и поясните величины, входящие в формулу.

– При каком условии I ~ U? Что это значит (что является функцией, а что аргументом в данном случае)?

• Экспериментальное доказательство прямо пропорциональной зависимости I (U).

Оборудование: три источника тока, амперметр, вольтметр, резистор, реостат, ключ, соединительные провода.

Приглашается экспертная группа (2 человека), которая опытным путём устанавливает связь между силой тока и напряжением: постепенно увеличивая число источников тока в цепи, следит за показанием приборов. Затем группа представляет классу отчёт (запись показаний приборов на доске, вид зависимости, график по данным эксперимента, вывод).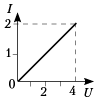

• Решение задач

– Дан график зависимости I (U). Определите значение силы тока при напряжении 4 В и рассчитайте сопротивление участка цепи.

– Постройте график зависимости силы тока в проводнике от напряжения, если при напряжении 6 В сила тока в проводнике 4 А. Масштаб выберите самостоятельною.

• Устная работа

Выразите из закона Ома сопротивление (R = U/I). Можно ли на этом основании считать, что сопротивление проводника прямо пропорционально напряжению и обратно пропорционально силе тока? От чего зависит сопротивление проводника? Как сопротивление проводника зависит от его длины? (R ~ l ). Что это значит? Имеются два проводника из одного и того же материала одинаковой площади поперечного сечения. Длина первого 20 см, второго 1 м. Сопротивление какого проводника больше и во сколько раз? (Второго, в 5 раз.) (Варианты: l₁ = 35 см; l₂ = 2,5 дм; l₁ = l₂, R₁ = R₂.)

– По внешнему виду двух проводников оцените ориентировочно их длину и сделайте вывод о зависимости сопротивления проводников от длины. (Ученику предлагаются несколько резисторов с заклеенными значениями сопротивлений, нужно сравнить свои выводы с надписями на резисторах.)

• Заслушивание отчёта экспертной группы о зависимости I (U).

IV. Самостоятельная работа

Сделаем небольшую паузу. Поменяем вид деятельности – выполним самостоятельную работу.

На доске записаны функции:

а) y = 2x + 3; b) y = 2x; c) y = 1/5x;

d) y = –5/x; e) y = x/3 + 1; f ) y = 5x;

g) y = 3/x; h) y = 0,5х; i ) y = –1/(2x);

j) y = 2x – 5; k) y = 3; l ) y = 6/x.

Запишите функции в тетрадь по вариантам:

1-й – функции прямой пропорциональности,

2-й – линейные функции,

3-й – функции обратной пропорциональности.

(Проверка письменной работы и выставление оценок.)

V. Случаи обратно пропорциональной зависимости в физике

Как сила тока в проводнике зависит от его сопротивления? При каком условии? (U = const.)

• Экспериментальное доказательство обратно пропорциональной зависимости I (R)

Оборудование: источник тока, амперметр, вольтметр, три резистора, реостат, ключ, соединительные провода.

Приглашается экспертная группа (2 человека), которая опытным путём устанавливает связь между силой тока и сопротивлением: постепенно увеличивая сопротивление участка цепи путём последовательного соединения одного, двух и трёх резисторов, снимает показания приборов. Затем группа представляет классу свой отчёт о проделанной работе (запись показаний приборов на доске, вид зависимости, график по данным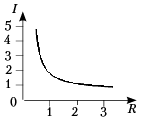 эксперимента, вывод).

• Решение задач

– По предложенному графику определите значения I₁, I₂, I₃ в цепи с одним резистором при R₁ = 0,5 Ом, R₂ = 1 Ом, R₃ = 2 Ом.

– По данной зависимости определите, какой из проводников имеет большее сопротивление.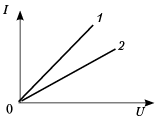

• Устная работа

– Как зависит сопротивление проводника от площади его поперечного сечения? Что это значит?

– По внешнему виду двух проводников оцените ориентировочно их площади сечения и сделайте вывод о зависимости сопротивления проводника от его площади сечения. (Ученику предлагаются несколько резисторов с заклеенными значениями сопротивлений, нужно сравнить свои выводы с надписями на резисторах.)

– После протягивания проволоки через воло чильный станок длина её увеличилась в три раза. Как изменилось сопротивление проволоки?

• Заслушивание отчёта экспертной группы о зависимости I (R).

VI. Графическое решение уравнений

На этом этапе урока вы научитесь применять свои знания при решении уравнений графическим способом, хотя алгебраически эти уравнения вы пока решать не умеете.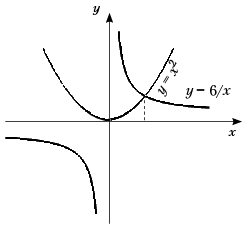

Например: x² = 6/x.

Зададим левую и правую части уравнения через функции: y₁ = x²; y₂ = 6/x и построим графики этих функций. D (y₁) = R, D (y₂) = R, x 0.

Абсцисса точки пересечения графиков и будет являться корнем уравнения x 1,8.

VII. Закрепление знаний

Решение № 622 из учебника «Алгебра-8» (можно вызвать ученика к доске).

VIII. Подведение итогов урока и выставление оценок

IX. Домашнее задание

Составьте кроссворд из понятий, которые изучили и повторили сегодня на уроке.