Тип занятия: комбинированное.
Цель: научить находить точку золотого
сечения на отрезке геометрическим и
алгебраическим методами.
Задачи:
— дать понятия целого и части предмета,
пропорции, ее обозначения;
— на примерах изобразительного искусства и
природных явлений продемонстрировать принцип
золотого сечения;
— дать историю понятия;
— показать значение золотого сечения для
изобразительного искусства
— развивать способность логически мыслить,
делать выводы, анализировать факты и события.
Наглядные материалы: мультимедийная
презентация в программе Power Point, произведения
графики из фондов ВМИИ.
Оборудование: столы, стулья, доска,
мультимедийный проектор, ноутбук, лист бумаги,
карандаш, линейка, циркуль.
Ход занятия
1. Подготовка
к
занятию, организация внимания учащихся (3 мин.)
2.
Постановка целей, выделение
дидактических задач занятия. Эмоциональный
настрой учащихся (2 мин.)
3.
Введение в тему (5 мин.)
Понятие о предмете. Часть и целое
Окружающие предметы мы различаем по
форме. Заинтересованность формой какого-либо
предмета может быть продиктована жизненной
необходимостью, а может быть вызвана и красотой
формы.

Фрагмент кирпичной стены
Целое всегда состоит из частей, части
разной величины находятся в определенном
отношении друг к другу и к целому.

Ворота богини Иштар в Вавилоне
Ведение понятия «золотое сечение»
Иоганн Кеплер говорил, что геометрия
владеет двумя сокровищами — теоремой Пифагора и
золотым сечением. И если первое из этих двух
сокровищ можно сравнить с мерой золота, то второе
с драгоценным камнем.
Теорему Пифагора знает каждый школьник, а что
такое золотое сечение — далеко не все.

Леонардо да Винчи. Автопортрет. Ок. 1512
4. Объяснение
нового
материала (20 мин.)
Что такое пропорция?
Соотношение целого и части может быть
выражено пропорцией. Пропорция — это равенство
двух отношений. Записывается пропорция с
помощью букв:
а : b = с : d или 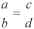
где а, b, с, d не равны нулю.
Читается: а так относится к b, как с относится к d; а
и d являются крайними членами пропорции, а b и с
средними ее членами.
Существует основное свойство пропорции: в верной
пропорции произведение крайних членов равно
произведению средних членов.
Деление отрезка на части
Золотое сечение — это такое
пропорциональное деление отрезка на неравные
части, при котором весь отрезок так относится к
большей части, как сама большая часть относится к
меньшей; или, другими словами, меньший отрезок
так относится к большему, как больший ко всему:
a : b = b : c или с : b = b : а.
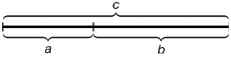
Нахождение точки золотого сечения на
отрезке с использованием теоремы Пифагора
Так как же можно найти точку золотого
деления отрезка? Возьмем любой отрезок AB и
предположим, что он равен единице. Где же
находится точка на отрезке, которая делит его на
две части в золотом сечении? Есть много способов
найти эту пропорцию. Мы попробуем найти золотое
сечение отрезка с помощью теоремы Пифагора.
Вы знаете, что уравнение прямоугольного
треугольника, имеет вид:
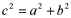 (1) (1)
где c — гипотенуза, a и b — катеты.
Возьмем треугольник, в котором больший катет
равен нашему отрезку АВ, длину которого мы
приняли за единицу. Меньший катет примем за
половину отрезка АВ, то есть 1/2 АВ. Подставив
значения катетов в формулу (1), мы
получим значение гипотенузы нашего
треугольника.
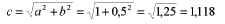
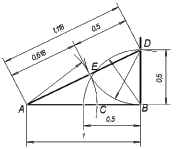
Поставив циркуль в точку D и проведя
дугу из точки B до пересечения со стороной AD,
получим точку E. Отнимем от длины отрезка AD = с = 1,118
радиус проведенной дуги, равной 0,5, получим
значение 0,618. Установив циркуль в точку А,
проведем дугу через точку Е до пересечения со
стороной АВ, получим точку С, делящую отрезок АВ в
золотом сечении.
Нахождение точки золотого сечения на
отрезке с помощью числа 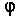 (фи) (фи)
Для проверки подставим полученные
значения в пропорцию, делящую отрезок в крайнем и
среднем положениях.

Полученное значение 1,618... есть
знаменитое число 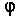 (фи), названное так американским
математиком Марком Барром по первой букве имени
великого Фидия, который, по преданию, часто
использовал золотое сечение в своих скульптурах. (фи), названное так американским
математиком Марком Барром по первой букве имени
великого Фидия, который, по преданию, часто
использовал золотое сечение в своих скульптурах.
Точку золотого сечения отрезка, зная его длину,
можно найти и арифметическим способом, используя
следующую формулу:
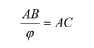 , ,
где АВ — длина отрезка, АС — длина до
точки золотого сечения.
Число 1,618… называемое золотым сечением, входит в
тройку самых известных иррациональных чисел, то
есть таких чисел, десятичные представления
которых бесконечны и непериодичны. Остальные
два: П (3,14...) — отношение длины
окружности к диаметру и е (2,71...) —
основание натуральных логарифмов. И, хотя
золотое сечение и не является таким же
фундаментальным в математике, как два других, оно
имеет большое значение для нашего восприятия
мира, так как пропорции, отвечающие золотому
сечению, кажутся нам гармоничными.
Исторический пример применения
золотого сечения в искусстве
 Считается, что первым
понятие о золотом
сечении ввел Пифагор. Возможно, Пифагор свое
знание позаимствовал у египтян и вавилонян. И
действительно, пропорции пирамиды Хеопса,
древних храмов, барельефов, предметов быта и
украшений свидетельствуют, что египетские
мастера пользовались соотношениями золотого
сечения при их создании. Французский архитектор
Ле Kорбюзье нашел, что в рельефе из храма фараонa
Cети I в Абидосе и в рельефе, изображающем фараона
Pамзеса, пропорции фигур соответствуют величинам
золотого сечения. Зодчий Хесира, изображенный на
рельефе деревянной доски из гробницы его имени,
держит в руках измерительные инструменты, в
которых зафиксированы пропорции золотого
сечения. Считается, что первым
понятие о золотом
сечении ввел Пифагор. Возможно, Пифагор свое
знание позаимствовал у египтян и вавилонян. И
действительно, пропорции пирамиды Хеопса,
древних храмов, барельефов, предметов быта и
украшений свидетельствуют, что египетские
мастера пользовались соотношениями золотого
сечения при их создании. Французский архитектор
Ле Kорбюзье нашел, что в рельефе из храма фараонa
Cети I в Абидосе и в рельефе, изображающем фараона
Pамзеса, пропорции фигур соответствуют величинам
золотого сечения. Зодчий Хесира, изображенный на
рельефе деревянной доски из гробницы его имени,
держит в руках измерительные инструменты, в
которых зафиксированы пропорции золотого
сечения.
Когда ученые в XIX в. начали сравнивать пропорции
сторон египетских пирамид, то обнаружили, что
знаменитое число 1,618… присутствует и в их
строениях. Например, если принять сторону
пирамиды, равную 2 единицам, то ее высота будет
равна 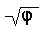 , а
высота грани самому числу , а
высота грани самому числу 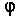 . .
Золотое сечение было известно древним грекам.
Античный циркуль
В эпоху Возрождения отношение,
выражаемое числом 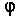 , называли «божественной пропорцией».
Много замечательных свойств , называли «божественной пропорцией».
Много замечательных свойств 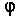 , проявляющихся в различных
плоских и пространственных фигурах, было собрано
в трактате Луки Пачиоли, вышедшем в 1509 году под
названием «De Divina Proportione» («О божественной
пропорции») с иллюстрациями Леонардо да Винчи. , проявляющихся в различных
плоских и пространственных фигурах, было собрано
в трактате Луки Пачиоли, вышедшем в 1509 году под
названием «De Divina Proportione» («О божественной
пропорции») с иллюстрациями Леонардо да Винчи.
Именно Леонардо ввел термин «золотая пропорция».
Под впечатлением от работы Пачиоли Леонардо сам
много работает над изучением золотого сечения и
на основании записок римского архитектора
Витрувия создает свою пропорцию человеческого
тела — известный рисунок «Витрувианский
человек». В то же время в Германии свою пропорцию
человека создает и Альбрехт Дюрер, который также
общался с Лукой Пачиоли.
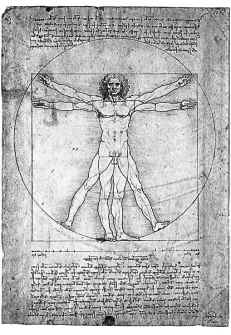
Леонардо да Винчи. Витрувианский
человек
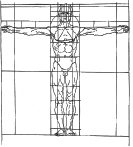 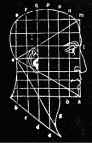
Пропорция Дюрера
А вновь «открыто» золотое сечение было
в середине XIX в. В 1855 г. немецкий исследователь
золотого сечения профессор Цейзинг опубликовал
свой труд «Эстетические исследования».
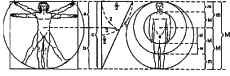
Пропорция Цейзинга
На практике обычно точку золотого
сечения находят, отложив на отрезке 62% от его
общей длины.
Число 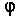 удивительным образом встречается в строении
живых организмов. Один из примеров — раковина.
Форма спирального завитка раковины привлекла
внимание Архимеда. Он изучал ее и вывел уравнение
спирали. В основе спирали лежат последовательно
вписываемые дуги в увеличивающиеся
прямоугольники золотого сечения. Увеличение
«шага» спирали всегда равномерно. В настоящее
время спираль Архимеда широко применяется в
технике.
удивительным образом встречается в строении
живых организмов. Один из примеров — раковина.
Форма спирального завитка раковины привлекла
внимание Архимеда. Он изучал ее и вывел уравнение
спирали. В основе спирали лежат последовательно
вписываемые дуги в увеличивающиеся
прямоугольники золотого сечения. Увеличение
«шага» спирали всегда равномерно. В настоящее
время спираль Архимеда широко применяется в
технике.
Еще Гёте подчеркивал тенденцию природы к
спиральности. Совместная работа ботаников и
математиков пролила свет на эти удивительные
явления природы. Выяснилось, что в расположении
листьев на ветке, семян подсолнечника, шишек
сосны проявляет себя закон золотого сечения.
Паук плетет паутину спиралеобразно. Спиралью
закручивается ураган. Испуганное стадо северных
оленей разбегается по спирали. Молекула ДНК
закручена двойной спиралью. Гёте называл спираль
«кривой жизни».
Среди придорожных трав растет ничем не
примечательное растение — цикорий. Приглядимся
к нему внимательно. От основного стебля
образовался отросток. Тут же расположился первый
листок. В росте и завоевании пространства это
растение сохраняет определенные пропорции.
Импульсы его роста постепенно уменьшаются в
пропорции золотого сечения.
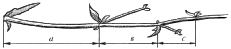
Рисунок цикория
В ящерице с первого взгляда
улавливаются определенные пропорции — длина ее
хвоста так относится к длине остального тела, как
62% к 38%.
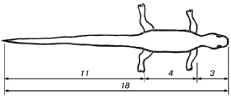
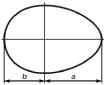
В частях проявляется повторение
строения целого. Примером может служить форма
яйца, в котором заключен глубокий смысл начала
мироздания.
Великий Гёте, поэт, естествоиспытатель
и художник (он рисовал и писал акварелью), мечтал
о создании единого учения о форме, образовании и
преобразовании органических тел. Это он ввел в
научный обиход термин «морфология». Пьер Кюри в
начале XX в. сформулировал ряд глубоких идей о
симметрии в природе. Он утверждал, что нельзя
рассматривать симметрию какого-либо тела, не
учитывая симметрию окружающей среды.
Закономерности «золотой» симметрии проявляются
в энергетических переходах элементарных частиц,
в строении некоторых химических соединений, в
планетарных и космических системах, в генных
структурах живых организмов. Эти закономерности,
как указано выше, есть в строении отдельных
органов человека и тела в целом, а также
проявляются в биоритмах и функционировании
головного мозга, сердца и зрительном восприятии.
 Золотая
пропорция оказывает влияние даже на
жизнеспособность машин. Например, в бесспорно
лучшем отечественном танке Великой
Отечественной войны Т-34 количество золотых
пропорций между частями не поддается подсчету! В
то же время, когда конструкторы начинают
забывать о золотой пропорции, это приводит к
печальным последствиям. В лучшем случае машины
выглядят негармонично.
Золотая
пропорция оказывает влияние даже на
жизнеспособность машин. Например, в бесспорно
лучшем отечественном танке Великой
Отечественной войны Т-34 количество золотых
пропорций между частями не поддается подсчету! В
то же время, когда конструкторы начинают
забывать о золотой пропорции, это приводит к
печальным последствиям. В лучшем случае машины
выглядят негармонично.
 Привлекательность золотой
пропорции
давно подметили художники. Чтобы передать свой
замысел, художник использует различные
композиционные приемы. В картине различают
геометрический и смысловой центр. Смысловой
центр художники часто располагают в пропорции
золотого сечения. Причем форма золотых пропорций
выбирается в зависимости от характера
произведения. Это могут быть линейные,
треугольные, прямоугольные, спиральные
композиции в золотом сечении, в зависимости от
характера и настроения, которого надо добиться. Привлекательность золотой
пропорции
давно подметили художники. Чтобы передать свой
замысел, художник использует различные
композиционные приемы. В картине различают
геометрический и смысловой центр. Смысловой
центр художники часто располагают в пропорции
золотого сечения. Причем форма золотых пропорций
выбирается в зависимости от характера
произведения. Это могут быть линейные,
треугольные, прямоугольные, спиральные
композиции в золотом сечении, в зависимости от
характера и настроения, которого надо добиться.
Что же представляет собой золотое
сечение в искусстве? Если деление по середине в
природе представлено, например, строением
кристаллов, а в искусстве характеризует покой,
равновесие и неподвижность, то деление по
золотому сечению выражает собой активность и
характеризует движение, развитие, ритм, оно —
свидетельство жизни.

Рафаэль. Афинская школа
5. Практическая
часть (10
мин.)
Нахождение точки золотого сечения на
отрезке
Практическое знакомство с золотым
сечением происходит в процессе деления отрезка
прямой в золотой пропорции и построения
спиральной линии в золотом прямоугольнике с
помощью циркуля и треугольной линейки. Ведущий
раздает слушателям по листу бумаги А4, карандаш,
циркуль и прямоугольный треугольник. На доске
ведущий последовательно производит
соответствующие построения:
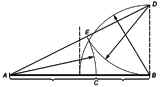
Из точки В проводится перпендикуляр,
равный половине АВ. Полученная точка D
соединяется линией с точкой А. На полученной
линии откладывается отрезок, равный ВD,
заканчивающийся точкой Е. Отрезок AЕ переносится
на прямую АВ. Полученная при этом точка С делит
отрезок АВ в соотношении золотой пропорции.
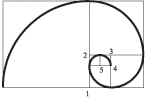
Построение спиральной линии
На листе бумаги чертится
прямоугольник со сторонами, равными 13 и 8 см.
Внутри прямоугольника с левой стороны
выделяется квадрат 8 X 8 см. Справа образуется
уменьшенный золотой прямоугольник со сторонами 8
и 5 см. В этом прямоугольнике также строится
квадрат со сторонами 5 см. Далее строим
соответственно квадраты со сторонами 3 и 2 см. В
конце остаются два квадрата со сторонами 1 см.
Всего получается шесть равномерно уменьшающихся
квадратов, вписанных в золотой прямоугольник.
Затем, последовательно устанавливая циркуль в
точки 1, 2, 3, 4, 5, проводим дуги в каждом из
квадратов.
6. Подведение
итогов
урока. Опрос-анкетирование (5 мин.)
| 
