«...Именно функция является тем
средством
математического языка, которое позволяет
описывать процессы движения, изменения,
присущие природе».
Г.Галилей
Цели:
- систематизация знаний о функциях;
- расширение математического кругозора;
- развитие познавательного интереса и творческой
активности.
Оборудование: таблицы, графики
функций,
карта звездного неба, модель простейшей
динамо-машины, портреты ученых.
Подготовка к занятию:
оформление
газет «Эрудит», «Звездный путь», кроссворд
«Функции», набор звезд и пентаграмм, доклады и
рефераты:
- Синус и синусоида в образах.
- Функциональные зависимости в природе.
- Свойства функций в народных пословицах.
План проведения
I. Постановка целей и задач.
II. Многообразие функциональных зависимостей.
III. Сообщение учащихся.
- Почему летом жарко?
- Синусоида в электротехнике.
IV. Свойства функций.
V. В мире открытий.
- Открытие Урана и астероидов.
- Звездное небо и логарифмы.
VI. Значимость изучения функциональных
зависимостей.
I. Постановка целей и задач.
Наш звездный час «Познай мир» посвящен
функциям. Значение их велико. Функции и реальный
мир неотделимы. Они описывают явления в природе.
Устанавливают закономерности, помогают
открывать законы, которые служат человечеству.
К этому занятию каждый из вас выполнил
определенную работу, которую продолжим сейчас.
Постепенно открывая пункты плана, которые
закрывают такие красивые звездочки, ведущие
подведут нас к заключительному этапу звездного
часа. ( План заранее написан на доске)
II. Многообразие функциональных
зависимостей.
Ведущий, убирая звездочку, читает написанные
на ней слова Галилея: «Именно функция является
тем средством математического языка, которое
позволяет описывать процессы движения,
изменения присущие природе».
Продолжает. « Функция выражает зависимость
между переменными величинами. Каждая область
знаний: химия, физика, биология, социология и др.
имеет свои объекты изучения, устанавливает
свойства и взаимосвязи между этими объектами в
реальном мире».
Ведущая. Впервые функция вошла в математику
под именем «переменная величина» в труде
французского математика и философа Рене
Декарта в 1637 г. Сам термин «функция»
впервые встречается в рукописи немецкого
математика и философа Г. Лейбница. Л. Эйлер
ввел принятые сейчас обозначения для функций.[3]
Сложный, очень длительный путь развития
понятия функции. С ним связаны имена Н.И. Лобачевского,
Л. Дирихле, Г. Кантора.
Ведущий. Сейчас многие науки берут на
вооружение математический аппарат. Такие
функциональные зависимости, например, возраст
деревьев, развитие амебы, развитие папоротника
изучает наука биология.
Функции помогают описывать процессы
механического движения тел, небесных и земных. С
помощью них ученые рассчитывают траектории
движения космических кораблей и решают
множество технических проблем.
Ведущая. Наряду с другими функциями,
тригонометрические занимают важное место.
Тригонометрия возникла из практических нужд
человека. Современный вид тригонометрии придал
крупнейший математик 18 столетия Леонард Эйлер.
Длительную историю имеет понятие синуса. Слово
косинус намного моложе. Тангенс, котангенс,
секанс, косеканс появились позднее.[3]
Принципиальное значение имело составление К.
Птолемеем первой таблицы синусов. Появилось
практическое средство решения ряда прикладных
задач.
Величины, меняющиеся по закону f(t) = Аcos (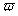 t + t +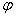 ) и f(t) = Аsin( ) и f(t) = Аsin(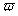 t + t +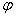 ) играют важнейшую роль
при описании любых колебательных процессов. ) играют важнейшую роль
при описании любых колебательных процессов.
Математический образ синусоиды можно получить,
рассматривая зависимость солнечной энергии от
угла падения на некоторый участок плоскости. Ведущий убирает вторую звездочку, читает на
ней: «О солнце! Без тебя не стало б в мире жизни».
После паузы продолжает: «Да будет свет!»
Выступления учащихся.
1. Почему летом жарко?
Причем здесь синусоида?
Многие считают, что летом жарче т.к. Земля
находится ближе всего к Солнцу, но это не так.
Орбита Земли - это почти круг, в центре которого
находится Солнце. И расстояние от Земли меняется
незначительно из месяца в месяц. Все дело в
наклоне земной оси по отношению к плоскости
земной орбиты. Зимой у нас Солнце невысоко
поднимается над горизонтом, его лучи лишь
скользят по земле. Летом Солнце приближается к
Зениту, лучи его падают почти отвесно. Поток
солнечной энергии одинаков во все времена. Он
зависит от угла падения лучей. Меняется угол
падения, меняется и доля Солнечной энергии. Зависимость
солнечной энергии от угла падения лучей и
выражает график у = sin x.[2]
2. Синусоида в электротехнике.
Откуда здесь берется синусоида? Простейшая
динамо-машина - источник переменного тока. Ток
возникает в рамке, которая равномерно вращается
в однородном магнитном поле. Так как рамка
вращается равномерно, то угол ее поворота может
служить мерой времени. Магнитный поток,
пронизывающий рамку, меняется во времени по
закону синуса. Оборот за оборотом – нарастания и
спады потока в точности повторяются снова и
снова. Так вдоль оси абсцисс одна за другой
выстраиваются волны синусоиды. Это график
магнитного потока.
Но ток в рамке определяется по скорости
изменения магнитного потока. Графиком является
синусоида, сдвинутая влево – косинусоида.
y = cosx = sin 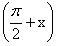 . [2] . [2] (разнообразные формы работы: групповая, парами,
индивидуальная).
1.Посторить график функции у = 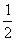 sin2x sin2x
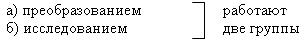
2. Построить схематически и перечислить
свойства: Е (f), Д(f), четкость, периодичность.
а) f (x)= 4sin 3x
б) f(x) =tg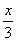 (двое у
доски, ведущие контролируют). (двое у
доски, ведущие контролируют).
3. Определить четкость, нечеткость функций,
написанных на доске, сделать вывод.
(работают остальные ребята)
- f (x) = tgx + x3,(нечетная)
- f (x) = tgx – x3, (нечетная)
- f (t)= x6 + cos x, (четная)
- f (x) = x6 – cosx, (четная)
Сумма и разность двух четных функций – четная
функция. Сумма и разность двух нечетных функций
– нечетная функция.
Проверяются второе и третье задания,
исправляются ошибки. Учитель просматривает
работу учащихся на месте, приглашает построить
на доске график функции y = 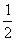 sin2x двух учеников (из каждой группы по
одному) и следит за их работой. sin2x двух учеников (из каждой группы по
одному) и следит за их работой.
«Звездная пауза»
Ведущие: «Определите ложные или истинные
высказывания»
Ложное – 0; истинное - 1.
№ |
Высказывания |
Ответы |
1 |
Синус является четной функцией |
0 |
2 |
Косинус функция четная |
1 |
3 |
Тангенс – нечетная функция |
1 |
4 |
Котангенс – четная функция |
0 |
5 |
Наименьший положительный период синуса
- 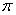 |
0 |
6 |
Косинус имеет наименьший положительный
период - 2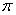 |
1 |
7 |
Тангенс имеет наименьший
положительныйпериод - 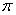 |
1 |
8 |
Котангенс имеет наименьший
положительный период - 2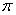 |
0 |
Взаимопроверка теста (ведущий читает
правильные ответы).
Учитель. Обратите внимание на графики,
построенные ребятами. Вы уже знаете, что их можно
построить разными способами. Проверим знание
свойств данной функции y= 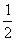 sin2x sin2x
На вопросы по графику отвечайте одним словом.
Один ученик отвечает у доски, записывая ответы.
На данном участке от -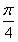 до до 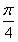 функция…
функция…
От 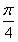 до до 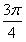 функция …. функция ….
В данной точке с координатами (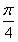 ; 0,5) - …. ; 0,5) - ….
В точке (- 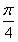 ; - 0,5) - …. ; - 0,5) - ….
Графиком этой функции является ….
Наука, изучающая тригонометрические функции ….
Ответы
- возрастает;
- убывает;
- максимум;
- минимум;
- синусоида;
- тригонометрия
Код правильного ответа, начиная со второй
буквы:
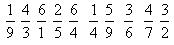
С первой буквы начинается имя знаменитого
ученого, теорема которого применяется при
решении различных задач (Пифагор).
Ответ. П Е Н Т А Г Р А М М А - символ школы
Пифагора, символ здоровья.
Ведущие всем присутствующим раздают
разноцветные пентаграммы. Ведущий убирает звездочку и читает
стихотворение Пушкина А.С.
О, сколько нам открытий чудных
Готовит просвещенья век!
1. Открытие Урана и астероидов.
Заслушивается сообщение ученика, об открытии Урана
и астероидов по правилу Тициуса – Боде r =
0,3•2n+0,4 , где r – среднее расстояние
планеты от Солнца. [1]
Планеты |
r |
Расстояние в а.е. |
| Меркурий |
0,4 |
0,39 |
| Венера |
0,7 |
0,72 |
| Земля |
1 |
1,00 |
| Марс |
1,6 |
1,52 |
| - |
2,8 |
- |
| Юпитер |
5,2 |
5,20 |
| Сатурн |
10 |
9,54 |
| Уран |
19,6 |
19,19 |
| Нептун |
38,8 |
30,07 |
| Плутон |
77,2 |
39,52 |
Ведущая снимает последнюю звезду со
словами М.В. Ломоносова:
Открылась бездна, звезд полна;
Звездам числа нет, бездне дна.
2.Звёздное небо и логарифмы.
Древнегреческий астроном Гиппарх насчитал на
небе около тысячи звезд и разбил их по видимому
блеску на шесть групп, самые яркие Гиппарх назвал
звездами первой величины, менее яркие – второй и
так далее в порядке равномерного убывания
видимого блеска – до звезд, едва видимых
невооруженным глазом, которым была присвоена
шестая величина. С изобретением чувствительных
приборов стало возможным точно определить блеск
звезд. Стало возможным сравнить, насколько
соответствует данным таких измерений
традиционное распределение звезд по видимому
блеску, произведенное на глаз.
По вертикальной оси будем откладывать блеск
звезды в единицах Гиппарха, то есть ее звездную
величину, по горизонтальной – показания
приборов. За масштабную единицу горизонтальной
оси принимается блеск звезды «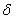 Тельца». Объективные
(прибор) и субъективные (глаз) характеристики
блеска не пропорциональны друг другу. Полученный
график называют графиком логарифмической
функции, которую предстоит изучить.[2] Тельца». Объективные
(прибор) и субъективные (глаз) характеристики
блеска не пропорциональны друг другу. Полученный
график называют графиком логарифмической
функции, которую предстоит изучить.[2]
Именно эта функция позволяет по массе
израсходованного топлива указать скорость
ракеты (формула К.Э. Циолковского).
VI. Значимость изучения функциональных
зависимостей.
Учитель. Сегодня мы проследили за
функциональными зависимостями в окружающем
мире. Оценили их роль в практической
деятельности человека, убедились в
необходимости изучения функции.
Кто–то из вас серьезнее будет относиться к
изучению математики, а некоторые займутся
исследовательской деятельностью. Удачи всем.
| 
