Цели:

Оформление:

1 страница. Историческая справка

«Лучше один раз увидеть, чем сто раз услышать» - гласит известная русская пословица.

Математический язык – это язык цифр, чисел, символов и рисунков.

Правильно выполненные рисунки, схемы, чертежи способны понять люди разных национальностей, здесь не существует языковых барьеров. Они могут заменить долгие разъяснения. Ведь верно выполненный рисунок к задаче залог верного ее решения. Уже в древности ученые научились заменять доказательства теорем геометрическим рисунком, чертежом.

Идея изображать числа в виде точек, а точкам давать числовые обозначения зародилась в далекой древности. Первоначальное применение координат связано с астрономией и географией, с потребностью определять положение светил на небе и определенных пунктов на поверхности Земли, при составлении календаря, звездных и географических карт. Следы применения идеи прямоугольных координат в виде квадратной сетки (палетки) изображены на стене одной из погребальных камер Древнего Египта.

2 страница. Прямоугольная система координат

Понятие прямоугольной системы координат на плоскости появилось в геометрии еще до начала нашей эры. С ее помощью математик Александрийской школы Апполоний определял и изучал кривые второго порядка – эллипс, гиперболу и параболу.

Простейшей из систем координат является числовая ось. Её легко получить из обычной прямой линии.

Координатная прямая – это прямая с указанными на ней началом отсчета, направлением отсчета и единичным отрезком. Числа, расположенные на координатной прямой справа от нуля, называются положительными, а слева – отрицательными

Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X'X и Y'Y. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление. Положительное направление осей (в правосторонней системе координат) выбирают так, чтобы при повороте оси X'X против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси Y'Y.

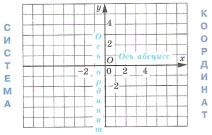
Четыре угла (I, II, III, IV), образованные осями координат X'X и Y'Y, называются координатными углами. Положение точки A на плоскости определяется двумя координатами x и y.. Координата x называется абсциссой точки , координата y — ординатой точки. Записывают так: А(х;у).

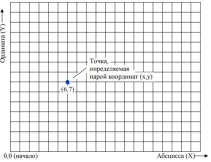
Если точка A лежит в координатном углу I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном углу II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном углу III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном углу IV, то точка A имеет положительную абсциссу и отрицательную ординату.

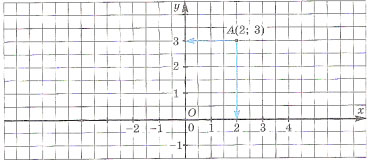
Чтобы определить координату точки надо из точки опустить перпендикуляр на координатные оси (ось абсцисс – х и ось ординат – у) и определить, какому числу координатной оси соответствует основание перпендикуляра. Для определения координаты точки А мы опускаем перпендикуляры на ось абсцисс – х и ось ординат – у. Полученная пара чисел (2;3) и есть декартовые координаты точки А (2;3).

3 страница. Рене Декарт

Рене Декарт (1596-1650) — французский философ, математик, физик и физиолог, основатель новоевропейского рационализма и один из влиятельнейших метафизиков Нового времени.

Декарт заложил основы аналитической геометрии, дал понятия переменной величины и функции, ввел многие алгебраические обозначения. Высказал закон сохранения количества движения, дал понятие импульса силы. Автор теории, объясняющей образование и движение небесных тел вихревым движением частиц материи (вихри Декарта). Р. Декарт ввел представление о рефлексе (дуга Декарта).

Рене Декарт родился 31 марта 1596, Лаэ, Турень, Франция.

Родившись в дворянской семье, Рене получил хорошее образование. В 1606 году отец отправил его в иезуитскую коллегию Ла Флеш. Учитывая не очень крепкое здоровье Декарта, ему делали некоторые послабления в строгом режиме этого учебного заведения, например, разрешали вставать позже других.

После окончания коллегии Декарт продолжил образование. В 1616 в университете Пуатье он получил степень бакалавра права. В 1617 Декарт поступает на службу в армию и много путешествует по Европе.

В 1620-е годы Декарт знакомится с математиком М. Мерсенном, через которого он долгие годы «держал связь» со всем европейским научным сообществом.

В 1649 году по приглашению шведской королевы Кристины Декарт отправился в Швецию. Суровый климат и непривычный режим (королева заставляла Декарта вставать в 5 утра, чтобы давать ей уроки и выполнять другие поручения) подорвали здоровье Декарта, и, подхватив простуду, он умер от пневмонии 11 февраля 1650, в Стокгольме.

Естественно-научные достижения Декарта родились как «побочный продукт» разрабатываемого им единого метода единой науки. Декарту принадлежит заслуга создания современных систем обозначений: он ввел знаки переменных величин (x, y, z...), коэффициентов (a, b, c...), обозначение степеней (a², x^-1...).

Декарт является одним из авторов теории уравнений: им сформулировано правило знаков для определения числа положительных и отрицательных корней, поставил вопрос о границах действительных корней и выдвинул проблему приводимости, т. е. представления целой рациональной функции с рациональными коэффициентами в виде произведения двух функций этого рода. Он указал, что уравнение 3-й степени разрешимо в квадратных радикалах (а также указал решение с помощью циркуля и линейки, если это уравнение приводимо).

Рене Декарт является одним из создателей аналитической геометрии (которую он разрабатывал одновременно с Пьером Ферма), позволявшей алгебраизировать эту науку с помощью метода координат. Предложенная им система координат получила его имя.

В работе «Геометрия» (1637), открывшей взаимопроникновение алгебры и геометрии, Декарт ввел впервые понятия переменной величины и функции. Переменная трактуется им двояко: как отрезок переменной длины и постоянного направления (текущая координата точки, описывающей своим движением кривую) и как непрерывная числовая переменная, пробегающая совокупность чисел, выражающих этот отрезок.

В область изучения геометрии Декарт включил «геометрические» линии (позднее названные Лейбницем алгебраическими) — линии, описываемые при движении шарнирными механизмами.

«Геометрия» оказала огромное влияние на развитие математики. В декартовой системе координат получили реальное истолкование отрицательные числа. Действительные числа Декарт фактически трактовал как отношение любого отрезка к единичному (хотя саму формулировку дал позднее И. Ньютон). В переписке Декарта содержатся и другие его открытия.

В оптике он открыл закон преломления световых лучей на границе двух различных сред (изложены в «Диоптрике», 1637). Р. Декарт внес серьезный вклад в физику, дав четкую формулировку закона инерции.

Созданный Декартом метод координат используется во всем мире и известен каждому школьнику.

4 страница. Рисунки на координатной плоскости. Практическая работа

При выполнении практических заданий надо быть очень внимательным, аккуратным, так как из-за неточности рисунок будет деформирован, искажен.

Задание1. На координатной плоскости построить точки по заданным координатам и последовательно соединить их отрезками.

(2;6), (-4;6), (-4;0), (0;0), (0;-3), (-2;-3), (-2;-2), (-4;-2), (-4;-4), (-3;-5), (1;-5), (2;-4), (2;1), (1;2), (-2;2), (-2;4), (2;4), (2;6)

Какая фигура при этом получилась?

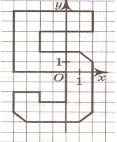
Задание 2. На координатной плоскости изобразите любую цифру и запишите координаты точек

Задание 3. На координатной плоскости построить точки по заданным координатам и последовательно соединить их отрезками.

(2;5), (8;5), (9;6), (9;3), (8;1), (6;2), (7;1), (1;1), (1;0), (10;-1), (13;0), (14;3), (14;1), (13;-1), (10;-2), (10;-3), (12;-5), (11;-8), (9;-8), (10;-6), (8;-5), (8;-7), (7;-8), (5;-8), (6;-7), (6;-5), (3;-5), (3;-8), (1;-8), (0;-5), (-1;-7), (-3;-8), (-3;3), (-4;3), (-4;-3), (-5;-4), (-7;-4), (-7;4), (-6;6), (-4;6), (-4;8), (-2;9), (0;9), (2;7), (2;5)

Какая фигура при этом получится?

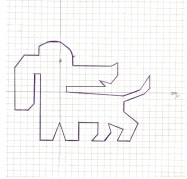
Задание 4. На координатной плоскости изобразите любую фигуру, рисунок и запишите координаты точек.

5 страница. Галерея рисунков на координатной плоскости (см. презентацию)

Вашему вниманию представлены авторские рисунки. Просмотрев галерею рисунков, попробуйте сами придумать рисунок и перенести его на координатную плоскость. Это очень интересная и в то же время очень трудная кропотливая работа, требующая от каждого внимательность и аккуратность, так как каждая неточность, ошибка приведут к искажению рисунка. Помните об этом при выполнении творческой работы. Творческих вам успехов.