Цели занятия:
- рассмотреть основные способы построения
графиков функций;
- познакомить со способами построения графиков
функций, содержащих модуль;
- познакомить со способам построения графика
кусочно – заданной функции;
- познакомить со способом построения графика
дробно – линейной функции.
Содержание:
1) у = – f(x).
2) y = f( – x).
3) y = f(x – a).
4) y = f(x) + b.
5) y = kf(x).
6) y = f(kx).
7) x = f(y).
8) y = | f(x) |.
9) y = f(| x |).
10) y = f(x) + g(x)
11) y = f(x) • g(x).
12) График кусочно – заданной функции.
13) График дробно – линейной функции.
14) Практическая исследовательская работа.
ХОД ЗАНЯТИЯ
1. С учащимися изучить карточку с описанием
основных способов построения графиков функций
Основные способы
построения графиков функций |
| 1) y = – f(x) |
График функции y = – f(x)
получается из графика функции y = f(x)
симметричным его отражением относительно оси Ох.
|
| 2) y = f(– x) |
График функции y = f(– x)
получается из графика функции y = f(x)
симметричным отражением его относительно оси Оу.
|
| 3) y = f(xa) – |
График функции y = f(x – a)
получается сдвигом вдоль оси Ох на величину | a
| графика функции y = f(x) вправо,
если a > 0, и влево, если a < 0. |
| 4) y = f(x) + b |
График функции y = f(x) + b
получается сдвигом графика функции y = f(x)
вдоль оси Оу на величину | b | вверх,
если b > 0, и вниз, если b < 0. |
| 5) y = kf(x) |
График функции y = kf(x) получается
растяжением в k раз , если k > 1, и
сжатием в 1/k раз, если 0 < k < 1, вдоль
оси Оу графика функции y = f(x). |
| 6) y = f(kx) |
График функции y = f(kx) получается
сжатием в k раз к оси Оу, если k > 1, и
растяжением в 1/k раз от оси Оу, если 0 < k
< 1, графика функции y = f(x). |
| 7) x = f(y) |
График функции x = f(y) симметричен
относительно прямой у = x графику
функции y = f(x).
У функции x = f(y): у –
независимая переменная, а х – зависимая
переменная. |
| 8) y = | f(x) | |
Для построения графика функции y = | f(x)
| надо сохранить ту часть графика функции y
= f(x), точки которой находятся на оси Ох
или выше оси Ох, и симметрично отразить
относительно оси Ох ту часть графика функции y
= f(x), которая расположена ниже оси Ох. |
| 9) y = f(| x |) |
Для построения графика функции y = f(| x
|) надо сохранить ту часть графика функции y =
f(x) точки которой находятся на оси Оу или
справа от нее и симметрично отразить эту часть
графика относительно оси Оу. |
| 10) y = f(x) + g(x)
|
Для построения графика функции y = f(x)
+ g(x) следует:
а) оставить только те точки графиков y = f(x)
и y = g(x), у которых х € Х, X =
D(f)
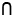 D(g); D(g);
б) произвести сложение ординат точек графиков y
= f(x) и y = g(x) для
каждого х
€ Х. |
| 11) y = f(x) • g(x)
|
Для построения графика функции y = f(x) • g(x)
следует:
а) оставить только те точки графиков y = f(x)
и y = g(x), у которых х € Х, X =
D(f)
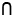 D(g); D(g);
б) произвести умножение ординат точек графиков y
= f(x) и y = g(x) для
каждого х
€ Х. |
2. Используя слайды презентации
познакомить учащихся с построением графиков
функций
1) y = – | x | . Слайд №3.
2) y = 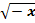 . Слайд
№4. . Слайд
№4.
3) y = | x – 2 | , y = | x + 2 | .
Слайд №5.
4) y = | x | – 2, y = | x | + 2.
Слайд №6.
5) y = 2 | x | , y = 1/2 | x | . Слайд №7.
6) y = 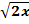 , y = , y = 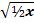 . Слайд №8. . Слайд №8.
7) x = y2. Слайд №9.
8) y = | x2 – 4 |. Слайд №10.
9) y = x2 – 4 | x | + 3. Слайд
№11.
10) y = | x – 2 | + | x + 2 | . Слайд
№12.
11) y = 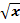 • •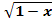 . Слайд №13. . Слайд №13.
12) у = 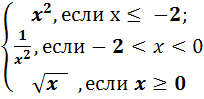 .
Слайд №14. .
Слайд №14.
13) y = 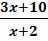 .
Слайд №15. .
Слайд №15.
3. Практическая исследовательская
самостоятельная работа
Задача №1. Построить график функции у
= 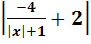 . .
Задача №2. Построить график функции у =
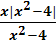 . .
4. Используя слайды презентации проверить
практическую работу
| 
