Цели урока:
- Развитие познавательной активности,
логического мышления учащихся.
- Обобщение и систематизация знаний и умений
учащихся по данной теме.
- Формирование умения применять полученные
знания в нестандартных ситуациях.
- Повышение мотивации обучения путем
использования инновационных технологий на
уроке.
Загрузить презентацию (795 КиБ)
Ход урока
I. Начало урока.
1). Организационный момент.
2). Домашнее задание.
3). Повторение основных вопросов теории.
II. Математический диктант. (с
использованием мультимедийного проектора )
(Презентация: слайд № 2 - 6 )
У каждого ученика на столе лежит листочек и
копирка. Задания выполняются под копирку, затем
один экземпляр сдается, а по другому ведется
проверка и обсуждение в классе.
Истинно или ложно каждое высказывание?
1) В арифметической прогрессии 2,4; 2,6;:: разность
равна 2 .
2) В геометрической прогрессии 0,3; 0,9;:: третий
член равен 2,7.
3) 11-й член арифметической прогрессии, у которой а1
= -4,2; d = 0,4, равен 0,2.
4) Сумма 5 первых членов геометрической
прогрессии, у которой b1= 1 q = - 2, равна 11.
5) Последовательность чисел, кратных 5, является
геометрической прогрессией.
6) Последовательность степеней числа 3 является
арифметической прогрессией.
III. Решение нестандартных задач.
(Презентация: слайд № 7-9)
В ходе математического диктанта мы повторили
определения арифметической и геометрической
прогрессий, формулы n-го члена, формулы суммы.
Были разобраны простейшие задачи на применение
этих формул. Но во всех этих задачах прогрессия
была задана, а найти нужно было какой-то ее член
или сумму.
А сейчас я хочу предложить вам обратную задачу.
1). Составьте арифметическую прогрессию, у
которой S3 = 60.
Обсуждение плана действий.
- С чего бы вы начали решать задачу, если нужно
было найти S3?
На доске записывается формула, далее
самостоятельное решение с последующей
проверкой.
Один ученик записывает на доске
последовательность и объясняет.
Кто еще составил последовательность, отличную
от этой?
Сколько существует таких прогрессий? Почему?
2). Существует ли такая арифметическая
прогрессия, в которой S3 = S5 ?
Да - нет ??? Мнения разделились.
Поднимите руку, кто считает, что существуют и
может это доказать.
Какой особенностью будет обладать эта
последовательность?
Один ученик у доски рассказывает свое решение.
Далее обсуждение других способов.
IV. Дидактические игры на уроке.
1). Математическое лото. (Презентация:
слайд № 10 - 15)
А теперь мы с вами поиграем. Разобьемся на три
команды - три ряда.
Для каждого ряда дается одна большая карта с
ответами. Каждый ученик получает маленькую
карточку с заданием (на каждой маленькой
карточке записана буква), решив ее, он выходит к
столу и кладет ее в нужное место (по ответу ) на
большой карте буквой наверх.
Карточки для учащихся составляются и раздаются
дифференцированно.
Большая карта:
| 1/ 9 |
1,2 |
215 |
- 2 |
| 4,1 |
1,2 |
5050 |
1/ 2 |
Карточки для учащихся:
А 1). ( аn ) - арифметическая прогрессия
а1= - 1, d = 0,2. Найти а12 .
К 2). ( вn ) - геометрическая прогрессия
в1 = 9, q =1/ 3. Найти в5.
Р 3). an = 3n + 5. Найти S10
Г 4) ( аn ) - арифметическая прогрессия
Найти 4-й член, если а3 = 3,2; а5 = 5.
С С 5). ( вn ) - геометрическая
прогрессия
Найти 5-й член, если в1 = 8; в3 = 2.
У 6).Найти сумму первых ста натуральных чисел.
А 7). Найти разность арифметической прогрессии,
если а4 = 2,4 ; а7 = 6.
Л 8). Найти знаменатель геометрической
прогрессии, если в3 =12; в5 =48 и все
её члены с нечётными номерами положительны, а с
чётными - отрицательны.
Побеждает та команда, которая первой заполнит
правильно свою большую карту.
2) Занимательная задача: "Выгодная сделка".
(Презентация: слайд № 16 - 19 )
Мистер Браун предложил мистеру Смитту сделку.
Она состояла в следующем: мистер Браун будет
ежедневно приносить мистеру Смитту по 100 тысяч
рублей. Не даром, разумеется, но плата пустяковая:
в 1 день Смитт ему за это заплатит - 1 копейку
во 2-й день за вторую сотню - 2 копейки
в 3-й день за третью сотню - 4 копейки
в 4 -й день:::::::.-::.8 копеек
и т.д., целый месяц, каждый день вдвое больше
предыдущего.
Договор не прерывать в течении месяца.
Смитт был счастлив: "А как же сотни тысяч за 1
копейку отдает ?!!".
Как вы считаете, для кого сделка оказалась
выгодной?
Далее идет обсуждение с классом.
| Дни месяца |
Мистер Смитт
(сотни тыс. руб.) |
Мистер Браун
( копейки ) |
| 1 |
100.000 |
1 |
| 2 |
100.000 |
2 |
| 3 |
100.000 |
4 |
| 4 |
100.000 |
8 |
| :. |
::::: |
Геометрич. прогрессия, q = 2 |
| 30 |
100.000 |
в30 |
| Доход: |
3.000.000 рублей |
S30=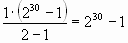 S30 = 10.737.418,23 рубля. |
Таким образом, сделка оказалась выгодной для
мистера Брауна.
Мистер Смитт принял его поначалу за глупого
человека, а Браун оказался достаточно умен, хитер
и хорошо разбирался в математике.
V. Итог урока.
Сегодня на уроке мы повторили определения
арифметической и геометрической прогрессий,
формулы n-го члена, суммы n первых членов.
Наряду с простейшими задачами разобрали
нестандартные задачи, поговорили о связи
математики с жизнью. Чтобы преуспеть в бизнесе,
нужно хорошо знать математику. Эти знания
помогут избежать невыгодных сделок.
Урок окончен. МОЛОДЦЫ!
| 
