Цели и задачи урока:
-образовательные - повторить алгоритм решения неравенств
второй степени методом интервалов, формировать навыки применения этого
алгоритма в нестандартных ситуациях;
-развивающие – развивать логическое мышление, способность
самостоятельно решать учебные задачи;
-воспитательные – прививать интерес к предмету, знакомить с
медиаресурсами на уроках математики, развивать сознательное восприятие
учебного материала
Оборудование:
-мультимедийный проектор;
-компьютер с необходимым программным обеспечением;
-раздаточный материал (карточки).
Ход урока
1.Организационный момент. (Эта часть
урока сопровождается презентацией).
2.Проверка домашнего задания устными
упражнениями.
(эта часть урока сопровождается презентацией)
3.Работа на доске и в тетрадях.
4.Дифференцированная самостоятельная работа,
(эта
часть урока сопровождается презентацией)
5.Подведение итогов,
(эта часть урока сопровождается
презентацией)
6.Коментарии по домашнему заданию.
1.Организационный момент.
Презентация используемая на уроке выполнена в программе Microsoft
Offise Power
Point 2003.Работает по щелчку.
Слайды №1,2,3,4,5.
Сообщение темы и цели
урока.
2.Проверка домашнего задания устными упражнениями
(сопровождается презентацией Слайд №6
)
а).Решить неравенства устно и записать на листках ответы к
каждому неравенству:
1). (х+2)(х-3)(х+5)>0
2.) (х-7)(х+5)?0

-5 -2 3
х -5
7 х
 
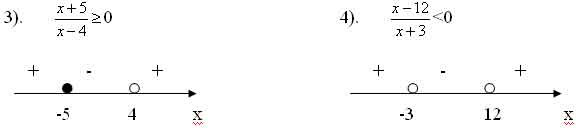
У 5 учащихся отобрать работы для оценки .
Ответы проверить с классом с помощью презентации: Слайд №6-выполнить
4-щелчка-на каждый щелчок появится 1 ответ.
1). (-5: -2)U(3: +?) 2). [-5;
7]
3). (-?; -5]U(4; +?)
4). (-3; 12)
б) Слайд№7.Рассказать алгоритм решения
неравенств второй степени методом интегралов:
-привести неравенство к виду (х-х1)(х-х2)
(х-хn)>0(<0), (1)
выделить функцию у=?(х)
-найти область определения функции
-найти нули функции, решив уравнение ?(х)=0
-отметить на оси Ох интервалы, на которых область определения
разбивается нулями функции. Определить знак функции на каждом
интервале.
3. Работа у доски и в
тетрадях Закрепление навыков в решении неравенств
методом интервалов.
Работаем по учебнику «Алгебра 9».
№ 136 (в, г). Найдите множество решений неравенства.
в). (х+12)(3-х)>0
Решаем, используя алгоритм.
Приведём неравенство к виду (1)
(х+12)(х-3)<0, выделим функцию
?(х)= (х+12)(х-3)
- Найдём D (?)= R
- Нули функции (х+12)(х-3)=0
х = -12; х=3
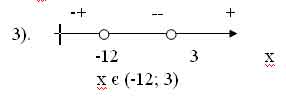
Ответ: (-12; 3)
г). (6+х)(3х-1)?0 Решаем, используя алгоритм:
приведем неравенство к виду (1), для этого во втором
двучлене вынесем 3 за скобки:
3 (х+6)(х-?)?0, выделим функцию
?(х)=3(х+6)(х-?)
1). Найдём D(?) = R
2).Нули функции 3(х+6)(х-?)=0
х1 =-6; х2 =?
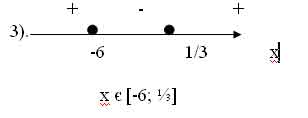
Ответ: [-6; ?]
№ 138 (а)
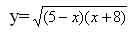
Область определения данной функции вытекает из условий,
что подкоренное выражение должно быть неотрицательным, т.е.
(5-х)(х+8)>=0
Решим неравенство, используя алгоритм.
Приведем данное неравенство к виду (1)
(х-5)(х+8) ?0, выделим функцию
?(х) = (х-5)(х+8)
1). D(?) = R
2).Нули функции (х-5)(х+8) =0
х1 =5; х2 =-8
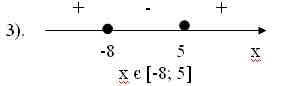
область определения данной функции: [-8; 5]
Ответ: [-8; 5]
4).Дифференцированная самостоятельная работа,
(рассчитанная на 15 минут)
Учащиеся получают трёхуровневые карточки с заданиями.(
Задание 1 –базового уровня, задание 2 –компетентного уровня, задание 3
–сложного уровня).(Карточки прилагаются ).
Учащиеся решают задания на отдельных листах, но ответы
дублируют себе в тетрадь.
По истечении 15 минут работы учащихся собираются. Ответы в своих тетрадях учащиеся проверяют с помощью презентации и
могут сразу оценить свою работу. Нормы оценок:
-за три выполненных примера - оценка «3»,
-за пять выполненных примеров – оценка «4»,
-за шесть выполненных примеров - оценка «5».,
Учитель сообщает оценки самостоятельной работы на следующем
уроке.
4). Подведение итогов.
1).Какая задача стояла перед нами в начале урока?
Можно ли считать, что мы ее решили.
2).Повторите алгоритм решения неравенств методом
интервалов.
5. Задание на дом.
| 
