Тип урока: урок применения знаний и умений.
Цели:
Обучающие:
- повторить все типы тригонометрических уравнений;
- отработать навыки решения различных типов уравнений;
- сформировать умение применять при решении уравнений нужный способ;
Методические: показать различные формы и методы контроля и самоконтроля качества усвоения знаний, умений и навыков учащимися;
Развивающие: развитие логического мышления через умение обобщать и систематизировать, доказывать и опровергать;
Воспитательные: воспитание настойчивости в приобретении знаний и умений, умения принимать самостоятельные решения.
Оборудование: интерактивная доска.
Ход урока
I. Вступительное слово учителя:
Сегодня ребята мы повторим с вами различные виды тригонометрических
уравнений, научимся проводить анализ заданий и способов их выполнения,
будем находить наиболее рациональные способы решения уравнений и
попытаемся самостоятельно оценить свои знания.
Прежде чем перейти непосредственно к нашей работе, мы сформируем
экспертную группу (3-4 человека), участники которой на втором этапе
нашего урока помогут мне оценить ваши знания, проверят домашние задания
и решения примеров классной работы, подведут итоги предстоящей устной
работы.
II. Устная работа.
1) На интерактивной доске появляется слайд со следующим текстом:

Задание: Назовите уравнения из второго столбца, решениями которых
являются выражения из первого столбца. Отметьте на доске при помощи
стрелок получившиеся соответствия.
При проверке на доске появляется слайд с тригонометрическим кругом,
учащиеся объясняют свой выбор, опираясь на выведенное изображение.
2) На интерактивной доске появляется слайд со следующим текстом:
- arcsin (–1) arctg (–1)
- arcsin
 arcos ( arcos ( ) ) - arcos
 arcsin arcsin  - arcos (–
 ) arcsin (– ) arcsin (–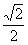 ) ) - arcsin
 arcsin arcsin 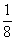
Задание: В тетради под номерами 1-5 впишите знаки сравнения, чтобы получились верные высказывания.
На доске появляется слайд с правильными ответами. Учащиеся отмечают,
сколько заданий они выполнили правильно. При помощи
тригонометрического круга дети обосновывают свой выбор.
3) На интерактивной доске появляется слайд со следующим текстом:

Задание: При помощи тригонометрического круга решите уравнения из
1-го столбца и установите соответствие с выражениями из второго
столбца.
На доске появляется слайд с правильными ответами. Учащиеся отмечают, сколько заданий они выполнили правильно.
4) Так как при решении тригонометрических уравнений постоянно
используются формулы и наша дальнейшая работа невозможна без знания
некоторых их них, то предлагаю вам проверить свои знания при помощи
диктанта.
Диктуем начало формул и предлагаем учащимся закончить их.
| I вар |
|
II вар |
| 1) sin 2x |
|
1) cos 2x |
| 2) sin (α + β) |
|
2) cos (α + β) |
| 3) cos α – cos β |
|
3) sin α – sin β |
| 4) sin x = a |
|
4) cos x = a |
5) cos2  |
|
5) sin2  |
На доске появляется слайд с правильными ответами и учащиеся, поменявшись тетрадями, проверяют работу соседа.
5) Учитель: Давайте вспомним, какие виды тригонометрических
уравнений мы знаем. Называя каждый вид, придумайте пример уравнения,
который ему соответствует.
- Уравнения, сводящиеся к квадратным.
- Уравнения, решаемые разложением на множители.
- Однородные уравнения.
- Уравнения, решаемые введением нового аргумента.
III. Решение тригонометрических уравнений.
1) Предлагаем учащимся уравнения, которые можно решить несколькими
способами, и вместе разбираем эти способы. Дети, предложившие тот или
иной способ, решают задания у доски.
1) cos x – cos 2x = 0
| I сп |
cos x – 2cos2x + 1 = 0
x = 2π.n,
x = ±  + 2.n, n є Z + 2.n, n є Z |
| II сп |
–2sin (–  )sin )sin  = 0 = 0
x = 2π.n,
x =  , n є Z , n є Z |
2) 3sin x – 2cos x = 3
| I сп |
6sin .cos .cos  – 2(cos2 – 2(cos2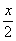 – sin2 – sin2 ) = 3(cos2 ) = 3(cos2 + sin2 + sin2 ) )
sin2 – 6sin – 6sin  . cos . cos  + 5cos2 + 5cos2 = 0 = 0
tg2 – 6tg – 6tg  +5 = 0 +5 = 0
tg  = 1, = 1,
x =  + 2π.k, k є Z + 2π.k, k є Z
tg
 = 5, = 5,
x = 2arctg 5 + 2π.n, n є Z |
| II сп |
 sin (x – arctg sin (x – arctg ) = 3 ) = 3
x – arctg  = (–1)k arcsin = (–1)k arcsin  + π.k, k є Z + π.k, k є Z
x = (–1)k arcsin  + π.k + arctg + π.k + arctg  , k є Z , k є Z |
Обращаем внимание на то, что решая уравнение разными способами, мы можем получить различные ответы.
2) Учитель: Сейчас я прошу вас сдать тетради экспертной группе,
которая приступит к проверке домашних заданий и подведет итоги проверки
и самопроверки устной работы.
Следующие задания вы будете выполнять на листах.
Каждый из вас получил карточку с уравнением. Обдумайте способ,
которым его можно решить. Проверьте, правильно ли вы выбрали способ.
Для этого переверните карточку и посмотрите на цифру внизу (заранее
дети не знают о том, что способ указан на карточке). После того как вы
решите уравнение, обратитесь в экспертную комиссию, которая проверит
правильность вашего решения. Обменяетесь карточкой со своим соседом,
проверьте друг у друга решения. Затем объединитесь в четверку с
учениками, сидящими за задней партой, решите уравнения, предложенные им,
проверьте решения.
| 1 |
8 cos2 x + 6 sin x – 3 = 0
8 (1-sin2 x) + 6 sin x – 3 = 0
8 sin2 x – 6 sin x – 5 = 0
sin x = t
8t – 6t – 5 = 0
t = 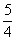 , ,
t = –
sin x =  – нет решений – нет решений
sin x = –
x = (–1)n+1  + π . n, n є Z + π . n, n є Z
|
|
| 2 |
3 sin2 x + sin x . cos x = 2 cos2 x / : cos2 x
3 tg2 x + tg x – 2 = 0
tg x = m
3m2 + m – 2 = 0
m = –1,
m = 
1) tg x = –1
x = arctg (–1) + π.n
x = – 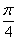 + π.n, n є Z + π.n, n є Z
2) tg x = 
x = arctg  + π.k, k є Z + π.k, k є Z
|
|
| 3 |
1 + cos x = –cos2 x
1 + cos x = – (2 cos2x – 1)
2 cos2x + cos x = 0
cos x (2 cos x + 1) = 0
1) cos x = 0
x = π/2 + π.n, n є Z
2) cos x = –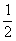
x = ± 2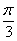 + 2π.k, k є Z + 2π.k, k є Z
|
|
| 4 |
cos 2x –  sin 2x = sin 2x = 
a2 + b2 =  2 = 2 2 = 2
 cos 2x – cos 2x –  sin 2x = sin 2x = 
sin Y cos 2x – cos Ysin 2x = 
sin (Y – 2x) = 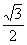
Y – 2x = (-1)n . 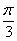 + π.n + π.n
–2x = (–1)n  – – 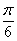 + π.n + π.n
x = (–1)n+1  + +  – –  , n є Z , n є Z
|
sin Y= 
Y = 
|
Учитель: Вы увидели, что в каждой четверке представлены все виды тригонометрических уравнений, о которых мы сегодня говорили.
Итак, подведем итоги. Сегодня мы повторили способы решения
простейших тригонометрических уравнений, вспомнили формулы и
определения обратных тригонометрических функций и способы их сравнения,
решали 4 вида тригонометрических уравнений разными способами и поняли,
что при решении разными способами необязательно получаются одинаковые
ответы. Кроме этого мы работали над своей самооценкой и оценивали своих
одноклассников. Предоставим слово экспертной комиссии. Выставляем
оценки за работу на уроке.
IV. Домашнее задание.
Учитель: Используя дополнительную литературу, учебник, свои знания,
придумайте 5 заданий для своих одноклассников, напишите их на отдельном
листе, не забыв предварительно решить. На следующем уроке мы проведем
самостоятельную работу, используя ваш материал, и вы сами проверите
работы своих товарищей.
| 
