Цели:
- Повторить понятия «спрос» и «предложение» и показать, как они
взаимодействуют в жизни.
- Развить умения использовать полученные знания в математике для
решения экономических задач и совершенствовать навыки и умения
экономического анализа.
- Расширить кругозор. Ориентация на экономические профессии.
Формировать навыки делового общения.
Организационные формы урока: малая дидактическая
игра «крестики-нолики» на этапе актуализации прежних знаний, деловая
игра «Производственное совещание» на этапе изучения нового материала,
самостоятельная работа на этапе закрепления изученного.
Оборудование: рабочие тетради по экономике для 8
класса, вопросы для игры «крестики-нолики», таблички с названиями
рабочих отделов для деловой игры,
План урока:
- Организационный момент (1 мин.)
- Постановка целей урока (5 мин.)
- Проверка усвоения пройденного материала (игра «крестики-нолики»,
15 мин.)
- Изучение нового материала с помощью интеграции экономики с
математикой (деловая игра «Производственное совещание», 40 мин.)
- Закрепление нового материала (самостоятельная работа, 20 мин.)
- Подведение итогов (5 мин.)
- Домашнее задание (3 мин.)
- Оценки за урок (1мин.)
Ход урока
1. Организационный момент.
Проверка готовности учащихся к уроку, настрой детей на работу
2. Постановка целей урока.
- Уметь определять параметры равновесного состояния спроса и
предложения.
- Определять результаты равновесного состояния.
3. Проверка усвоение пройденного материала .
Вначале урока необходимо актуализировать знания ребят по темам
«спрос» и «предложение».
Игра «крестики-нолики». Дома учащиеся, разделенные
на две команды – «крестики» и «нолики», должны были подготовить
вопросы по пройденным темам: «Спрос» и «Предложение».
- команда – «Крестики» – подготовили вопросы по проблеме «спрос»
- команда – «Нолики» – подготовили вопросы по проблеме
«предложение».
Команда, которая по жребию получает право первого хода (предположим
«крестики»), выбирает номер клетки (например, а-1), команда-соперник
задает вопрос (приложение 3 у автора), соответствующий данному номеру.
Команда («крестики») отвечает, если ответ верный, то в выбранную клетку
ставится значок команды («Х»), если нет, то на свой вопрос отвечает
команда, задающая вопрос, и также в случае правильного ответа в данную
клетку ставится знак команды давшей правильный ответ («О»). Если обе
команды отвечают неверно, то клетка остается пустой. Победитель
определяется также как и в игре «крестики-нолики» (выигрывает та
команда, которая быстрее закроет своими знаками вертикальную или
горизонтальную строку, либо диагональ игрового поля, или наберет
большее количество крестиков или ноликов).
Рисунок 1
4. Изучение нового материала с помощью интеграции экономики
с математикой.
Учитель: До сих пор мы изучали поведение
потребителей и производителей обособленно друг от друга. Но в жизни
понятие спроса и предложения тесно взаимосвязаны. Ведь, чтобы заключить
сделку, продавцу и покупателю необходимо договориться и о цене и о
количестве товара, которые устраивали бы обоих. Таким образом, в
результате взаимодействия спроса и предложения на рынке возникает
ситуация рыночного равновесия:
Равновесие – это совпадение интересов продавца и
покупателя.
Эта ситуация характеризуется двумя величинами:
Равновесной ценой – ценой, по которой продавец еще
готов продать, а покупатели уже готовы купить товар;
и
Равновесным количеством
– количеством сделок по
равновесной цене.
Сегодня на уроке мы научимся определять эти равновесные параметры, а
также рассмотрим еще одну проблему. А какую вы узнаете, если
разгадаете шараду:
Первый слог – местоименье
Без второго нет грамоте ученья.
Если вместе соберешь
Цель труда производителя найдешь.
(Вы – ручка)
Но цель любого производителя – это получение не просто дохода
(выручки), а максимального дохода. Разобраться в этих непростых
вопросах нам поможет царица наук – Математика.
Деловая игра «Производственное совещание»
Проведем деловую игру «Производственное совещание»
(Для проведения игры учащиеся заранее были разделены на рабочие
группы по 4-5 человек по способностям: 1 гр. – экономисты; 2 гр. –
математики; 3 гр. – маркетологи; 4 гр. – отдел рекламы. Директор
предприятия – учитель экономики или математики).
Директор: Представим, что все мы работники
Шатковского молочного завода. За последнее время ситуация на нашем
заводе сложилась довольно сложная. Я прошу главного экономиста
подробнее разъяснить ситуацию и ввести всех нас в курс дела.
Экономист: Мы на предприятии ввели новую
технологическую линию по производству йогуртов, с целью расширения
ассортимента нашей продукции. Заключили договор о поставках сырья с
ближайшими совхозами, что позволяет снизить транспортные затраты и
повысить качество сырья за счет современной технологии. Но выручка не
растет.
Директор: Я прошу маркетологов дать свое заключение
по этому вопросу.
Маркетолог: Мы провели большую работу по изучению
ситуации на рынке. Отчет о наших исследованиях представлен в таблице:
| Р, руб. |
Qd, сот. штук |
Qs, сот. штук |
| 3 |
7 |
1 |
| 4 |
6 |
3 |
| 6 |
4 |
7 |
| 7 |
3 |
9 |
| 9 |
1 |
13 |
| 10 |
0 |
15 |
Директор: Я попрошу специалиста математика
конкретизировать данную ситуацию.
Математик 1: На основе имеющихся данных построим
графики спроса и предложения на одной координатной плоскости.
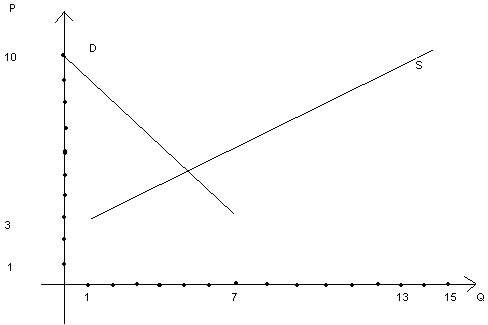
Рисунок 2
В параметрах Р = 5 р. Q= 500шт. эти графики пересеклись, т.е. точка
Е – общая точка графиков D и S .
Директор: Получается, что при цене в 5 рублей и
величине спроса 500 штук величина спроса равна величине предложения?
Экономист: Да, при таких значениях цены и
количества на рынке устанавливается равновесие, то есть Математик 2: Эти же параметры можно получить если
исследовать данные маркетологов аналитически. Выведем формулы
зависимости величины спроса и величины предложения от цены:
Пусть:
P1=3 P2=4
Qd1=7 Qd2=6
Qs1=1 Qs2=3;
зная, что спрос и предложение имеют линейную зависимость от цены,
составим уравнения: Qd= kP+ b
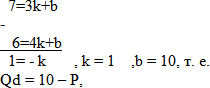
аналогично
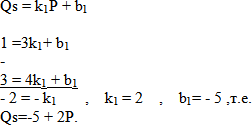
Определим равновесные параметры Qd = Qs
10 – P = - 5 + 2P
15 = 3P
Pe = 5, подставим в уравнение и найдем Qe = 500
Директор: Спасибо математикам за подробное
разъяснение. Но нас еще интересует выручка. Будет ли она максимальной
при таких значениях P и Q?
Экономист: Чтобы определить выручку нужно P*Q.
TRe = Pe* Qe
TRe= 5*500=2500 руб.
Математик 3: Чтобы ответить на второй вопрос:
«Будет ли она максимальной?» нужно провести исследование функции
выручки. Для этого сначала переведем известную нам функцию спроса в
обратную функцию Qd = 10 – P ===> Pd = 10 – Q
(Qs = 2P – 5 ===> Ps = 0,5Q – 2,5 )
TR = Pd *Q, образуем функцию выручки TR = (10 – Q)* Q = 10Q – Q2
– получили квадратичную функцию. Исследуем ее. Графиком данной функции
является парабола, ветви которой направлены вниз. Значит наибольшее
значение эта функция примет в точке являющейся вершиной этой параболы.
Определим ее координаты: 10Q – Q2 = TR
TRmax при Q = -10/-2 = 5 , подставим и определим Р
P = 10 – Q = 10 – 5 = 5(p) , TRmax = 5*500 =2500(руб.)
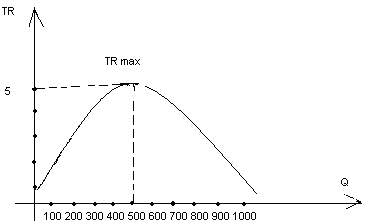
Рисунок 3
Экономист: Сравним TRe и TRmax.
Эти значения совпали, т.е. в сложившейся ситуации наша выручка
является наибольшей.
Директор: какие еще есть предложения по увеличению
выручки.
Маркетолог: Мы предлагаем увеличить
равновесную цену, но сохранить равновесный объем. Для
этого необходимо повысить спрос на продукцию, проведя большую рекламную
компанию, но в то же время, сократив предложение в таких же пропорциях.
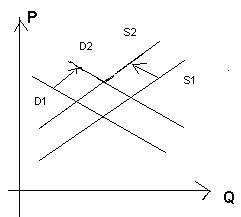
Рисунок 4
Директор: Итак, даем задание рекламному отделу:
провести рекламную компанию с целью повышения спроса на наши йогурты. А
по результатам этой компании сделаем дополнительную оценку состояния с
выручкой.
Рекламный отдел показывает подготовленную рекламу.
Директор: На сегодняшний день ситуация разъяснилась.
Всем спасибо. За работу, друзья.
5. Самостоятельная работа.
Учитель: Сегодня мы с вами увидели, что наибольшая
выручка получается продавцом в точке равновесия. А всегда ли это так?
Чтобы ответить на этот вопрос я предлагаю вам самостоятельно решить
задачу:
Даны функции спроса Qd = - 2P+ 13 и предложения Qs = 5P –
18.Определить TRe и TRmax и сравнить полученные
результаты.
Дети выполняют самостоятельную работу. (Ответ: TRe=18,35
p. TRmax=21,125 p)
Учитель:Как видите, в данном примере выручка в
точке равновесия и максимальное ее значение не совпадают. Какой можно
сделать вывод? (Значения выручки в точке равновесия и максимальное ее
значение не всегда равны между собой. Это обязательно нужно проверять с
помощью расчетов.)
6. Подведение итогов урока:
Что вы узнали нового сегодня на уроке?
Какие знания вам сегодня помогли в работе?
Какие основные выводы вы можете сделать?
7. Домашнее задание.
8. Оценки за урок.
| 
