Материал разработан на 2 спаренных урока.

Цели уроков: Сформировать у учащихся понимание вероятности, равновероятных событий и событий с различными вероятностями. Научить находить количество информации, используя вероятностный подход. Создать в Excel информационную модель для автоматизации процесса вычислений в задачах на нахождение количества информации, используя формулу Шеннона.

Требования к знаниям и умениям:

Учащиеся должны знать:

Учащиеся должны уметь:

Оборудование: доска, компьютер, мультимедийный проектор, карточки с заданиями, карточки-памятки, справочный материал.

Урок 1. Вероятностный подход к определению количества информации. Формула Шеннона

Ход урока

I. Организационный момент.

II. Проверка домашнего задания.

III. Постановка цели урока.

Задача: Какое сообщение содержит большее количество информации?

Первые три варианта учащиеся решают без затруднения. События равновероятны, поэтому можно применить для решения формулу Хартли. Но третье задание вызывает затруднение. Делаются различные предположения. Роль учителя: подвести учащихся к осмыслению, что в четвертом варианте мы сталкиваемся с ситуацией, когда события неравновероятны. Не все ситуации имеют одинаковые вероятности реализации. Существует много таких ситуаций, у которых вероятности реализации различаются. Например, если бросают несимметричную монету или "правило бутерброда".

Сегодня на уроке мы должны ответить на вопрос: как вычислить количество информации в сообщении о неравновероятном событии.

IV. Объяснение нового материала.

Для вычисления количества информации в сообщении о неравновероятном событии используют следующую формулу: I=log₂(1/p)

где I – это количество информации, р – вероятность события.

Вероятность события выражается в долях единицы и вычисляется по формуле: р=K/N,

где К – величина, показывающая сколько раз произошло интересующее нас событие, N – общее число возможных исходов какого-то процесса.

Вернемся к нашей задаче.

Пусть К₁ – это количество пирожков с повидлом, К₁=24

К₂ – количество пирожков с капустой, К₂=8

N – общее количество пирожков, N = К₁ +К₂=24+8=32

Вычислим вероятность выбора пирожка с разной начинкой и количество информации, которое при этом было получено.

Вероятность выбора пирожка с повидлом: р₁=24/32=3/4=0,75.

Вероятность выбора пирожка с капустой: р₂=8/32=1/4=0,25.

Обращаем внимание учащихся на то, что в сумме все вероятности дают 1.

Вычислим количество информации, содержащееся в сообщении, что Маша выбрала пирожок с повидлом: I₁=log₂(1/p₁)= log₂(1/0,75)= log₂1,3=1,15470 бит.

Вычислим количество информации, содержащееся в сообщении, если был выбран пирожок с капустой: I₂=log₂(1/p₂)= log₂(1/0,25)= log₂4=2 бит.

Пояснение: если учащиеся не умеют вычислять значение логарифмической функции, то можно использовать при решении задач этого урока следующие приемы:

Приложение 1. «Количество информации в сообщении об одном из N равновероятных событий: I= log₂N». (Приложение вы можете получить у автора статьи.)

При сравнении результатов вычислений получается следующая ситуация: вероятность выбора пирожка с повидлом больше, чем с капустой, а информации при этом получилось меньше. Это не случайность, а закономерность.

Качественную связь между вероятностью события и количеством информации в сообщении об этом событии можно выразить так: чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии.

Вернемся к нашей задаче с пирожками. Мы еще не ответили на вопрос: сколько получим информации при выборе пирожка любого вида?

Ответить на этот вопрос нам поможет формула вычисления количества информации для событий с различными вероятностями, которую предложил в 1948 г. американский инженер и математик К.Шеннон.

Если I-количество информации, N-количество возможных событий, р_i - вероятности отдельных событий, где i принимает значения от 1 до N, то количество информации для событий с различными вероятностями можно определить по формуле:

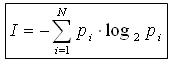
можно расписать формулу в таком виде:

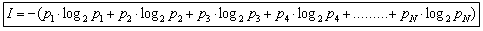
Рассмотрим формулу на нашем примере:

I = - (р₁∙log₂p₁ + р₂∙log₂p₂)= - (0,25∙ log₂0,25+0,75∙ log₂0,75)≈-(0,25∙(-2)+0,75∙(-0,42))=0,815 бит

Теперь мы с вами можем ответить на вопрос задачи, которая была поставлена в начале урока. Какое сообщение содержит большее количество информации?

Ответ: в 1 сообщении.

Обратите внимание на 3 и 4 задачу. Сравните количество информации.

Мы видим, что количество информации достигает максимального значения, если события равновероятны.

Интересно, что рассматриваемые нами формулы классической теории информации первоначально были разработаны для технических систем связи, призванных служить обмену информацией между людьми. Работа этих систем определяется законами физики т.е. законами материального мира. Задача оптимизации работы таких систем требовала, прежде всего, решить вопрос о количестве информации, передаваемой по каналам связи. Поэтому вполне естественно, что первые шаги в этом направлении сделали сотрудники Bell Telephon Companie – X. Найквист, Р. Хартли и К. Шеннон. Приведенные формулы послужили К. Шеннону основанием для исчисления пропускной способности каналов связи и энтропии источников сообщений, для улучшения методов кодирования и декодирования сообщений, для выбора помехоустойчивых кодов, а также для решения ряда других задач, связанных с оптимизацией работы технических систем связи. Совокупность этих представлений, названная К. Шенноном "математической теорией связи”, и явилась основой классической теории информации. (Дополнительный материал можно найти на сайте http://polbu.ru/korogodin_information или прочитав книгу В.И. Корогодин, В.Л. Корогодина. Информация как основа жизни. Формула Шеннона.)

Можно ли применить формулу К. Шеннона для равновероятных событий?

Если p₁=p₂=..=p_n=1/N, тогда формула принимает вид:

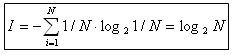
Мы видим, что формула Хартли является частным случаем формулы Шеннона.

V. Закрепление изучаемого материала.

Задача: В корзине лежат 32 клубка красной и черной шерсти. Среди них 4 клубка красной шерсти.

Сколько информации несет сообщение, что достали клубок красной шерсти? Сколько информации несет сообщение, что достали клубок шерсти любой окраски?

Дано: К_к=4;N=32

Найти: I_к, I

Решение:

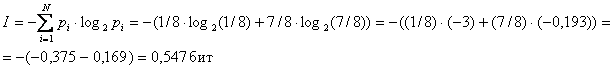
Ответ: I_к=3 бит; I=0,547 бит

VI. Подведение итогов урока.

Вопросы:

Урок 2. Применение ЭТ Excel для решения задач на нахождение количества информации

Пояснение: При решении задач на нахождение количества информации учащиеся не вычисляли значение логарифма, т.к. не знакомы с логарифмической функцией. Урок строился таким образом: сначала решались однотипные задачи с составлением формул, затем разрабатывалась табличная модель в Excel, где учащиеся делали вычисления. В конце урока озвучивались ответы к задачам.

Ход урока

I. Постановка целей урока

На этом уроке мы будем решать задачи на нахождение количества информации в сообщении о неравновероятных событиях и автоматизируем процесс вычисления задач данного типа.

Для решения задач на нахождение вероятности и количества информации используем формулы, которые вывели на прошлом уроке:

р_i=K_i/N; I_i=log₂(1/p_i);

II. Решение задач.

Ученикам дается список задач, которые они должны решить.

Задачи решаются только с выводами формул, без вычислений.

Задача №1

В озере обитает 12500 окуней, 25000 пескарей, а карасей и щук по 6250. Какое количество информации несет сообщение о ловле рыбы каждого вида. Сколько информации мы получим, когда поймаем какую-нибудь рыбу?

Дано: К_о=12500; К_п=25000; К_к= К_щ=6250

Найти: I_о, I_п, I_к, I_щ, I

Решение:

III. Объяснение нового материала.

Задается вопрос ученикам:

1. Какие трудности возникают при решении задач данного типа? (Отв.: Вычисление логарифмов).

2. Нельзя ли автоматизировать процесс решения данных задач? (Отв.: можно, т.к. алгоритм вычислений в этих задачах один и тот же).

3. Какие программы используются для автоматизации вычислительного процесса? (Отв.: ЭТ Excel).

Давайте попробуем сделать табличную модель для вычисления задач данного типа.

Нам необходимо решить вопрос, что мы будем вычислять в таблице. Если вы внимательно присмотритесь к задачам, то увидите, что в одних задачах надо вычислить только вероятность событий, в других количество информации о происходящих событиях или вообще количество информации о событии.

Мы сделаем универсальную таблицу, где достаточно занести данные задачи, а вычисление результатов будет происходить автоматически.

Структура таблицы обсуждается с учениками. Роль учителя обобщить ответы учащихся.

При составлении таблицы мы должны учитывать:

Прежде чем демонстрировать заполнение таблицы, учитель повторяет правила ввода формул, функций, операцию копирования (домашнее задание к этому уроку).

При заполнении таблицы показывает как вводить логарифмическую функцию. Для экономии времени учитель демонстрирует уже готовую таблицу, а ученикам раздает карточки-памятки по заполнению таблицы.

Рассмотрим заполнение таблицы на примере задачи №1.

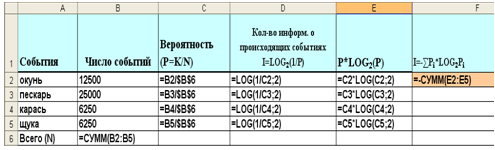
Рис. 1. Режим отображения формул

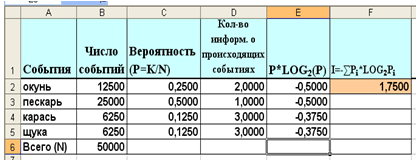
Рис. 2. Отображение результатов вычислений

Результаты вычислений занести в тетрадь.

Если в решаемых задачах количество событий больше или меньше, то можно добавить или удалить строчки в таблице.

VI. Практическая работа.

1. Сделать табличную модель для вычисления количества информации.

2. Используя табличную модель, сделать вычисления к задаче №2 (рис.3), результат вычисления занести в тетрадь.

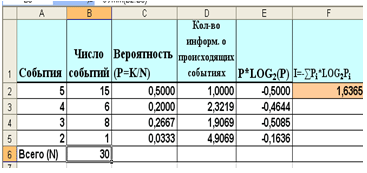
Рис. 3

3. Используя таблицу-шаблон, решить задачи №3,4 (рис.4, рис.5), решение оформить в тетради.

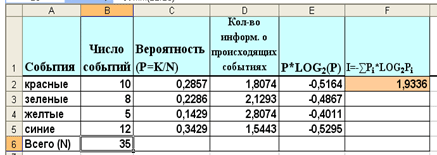
Рис. 4

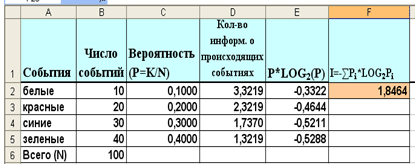
Рис. 5

4. Сохранить таблицы в своих папках под именем «инф_вероятность».

Задача №2

В классе 30 человек. За контрольную работу по информатике получено 15 пятерок, 6 четверок, 8 троек и 1 двойка. Какое количество информации несет сообщение о том, что Андреев получил пятерку?

Задача№3

В коробке лежат кубики: 10 красных, 8 зеленых, 5 желтых, 12 синих. Вычислите вероятность доставания кубика каждого цвета и количество информации, которое при этом будет получено.

Задача№4

В непрозрачном мешочке хранятся 10 белых, 20 красных, 30 синих и 40 зеленых шариков. Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика?

VII. Подведение итогов урока.

Учитель оценивает работу каждого ученика. Оценивается не только практическая работа на компьютере, но и оформление решения задачи в тетради.

VIII. Домашняя работа.

1. Параграф учебника «Формула Шеннона», компьютерный практикум после параграфа.

2. Доказать, что формула Хартли – частный случай формулы Шеннона.