Цели:
- формирование навыков составления алгоритмов с
ветвлениями, работы с алгоритмами, содержащими
ветвления;
- закрепление навыков по составления алгоритмов
с ветвлениями, самостоятельной работы и работы в
группе.
Задачи:
- учебная – формирование практических навыков
разработки алгоритмов с ветвлениями и
вычислений по алгоритмам с ветвлениями;
- развивающая – развитие алгоритмического
мышления, памяти, внимания, логического мышления,
познавательного интереса, коммуникативной
культуры, учебно-познавательной компетенции;
- воспитательная – развитие познавательного
интереса, способствовать воспитанию в детях
милосердия, ответственности, взаимопонимания,
взаимоуважения, взаимопомощи и поддержки.
Оборудование и программное обеспечение:
текстовый редактор MS-Word, презентации PowerPoint.
План урока:
- Организационный момент.
- Контроль знаний.
- Объяснение нового материала.
- Закрепление.
- Итог урока.
Ход урока
1. Организационный момент.
Приветствие. Проверка присутствующих.
Установление психологического и эмоционального
контакта с детьми.
2. Контроль знаний.
- Вспомните, какие вопросы мы рассмотрели на
прошлом уроке.
- Что называется "ветвлением”?
- Какие способы оформления ветвлений мы узнали?
- Какие формы ветвлений вам известны?
- Как выглядят блок-схемы алгоритмов с
ветвлениями?
Задания для работы в группах:
1 группа: Составьте блок-схему к алгоритму
1.
Алгоритм 1:
Уменьшить скорость.
Если ремонт дороги закончен, то проехать 2 км по
отремонтированному участку дороги к офису, иначе
проехать 5 км в объезд.
Конец ветвления.
Остановиться возле офиса.
2 группа: Составьте блок-схему к алгоритму
2.
Алгоритм 2:
Подойти к кассе.
Если билеты на сеанс 12.00 имеются, то:
Протянуть кассиру деньги.
Назвать сеанс и количество билетов.
Получить билеты.
Конец ветвления.
Отойти от кассы.
3 группа: Составьте блок-схему к алгоритму
по нахождению корней квадратного уравнения. (ax2+bx+c=0).
После выполнение заданий на экране решение
задания группы 3:
Алгоритм 3:
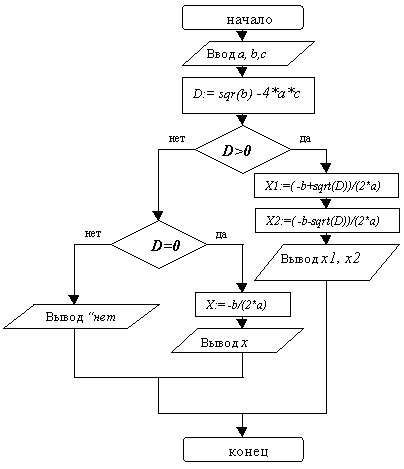 Алг yrav; Алг yrav;
a, b,с:цел;
d,x1,x2,x: вещ;
Нач
Ввод a, b,c;
D:= sqr(b) -4*a*c ;
Если D>0, то
X1:=( -b+sqrt(D))/(2*а);
Х2:=( -b-sqrt(D))/(2*а);
Вывод X1, Х2
Иначе
Если D=0, то
X:= -b/(2*а);
Вывод X
Иначе
Вывод "корней нет”;
Кв;
Кв;
Кон.
Обратить внимание, что алгоритм может
выглядеть иначе:
Алгоритм 3:
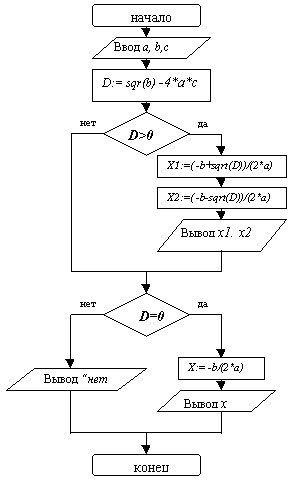 Алг yrav1; Алг yrav1;
a, b,с:цел;
d,x1,x2,x: вещ;
Нач
Ввод a, b,c;
D:= sqr(b) -4*a*c ;
Если D>0, то
X1:=( -b+sqrt(D))/(2*а);
Х2:=( -b-sqrt(D))/(2*а);
Вывод X1, Х2;
Кв;
Если D=0, то
X:= -b/(2*а);
Вывод X
Иначе
Вывод "корней нет”;
Кв;
Кон.
3. Объяснение нового материала.
Сегодня на уроке мы рассмотрим, каким образом
действует исполнитель по алгоритмам, содержащим
ветвления. Рассмотрим задачу:
Задача 1. Найдите значение переменной S
после выполнения следующего алгоритма.
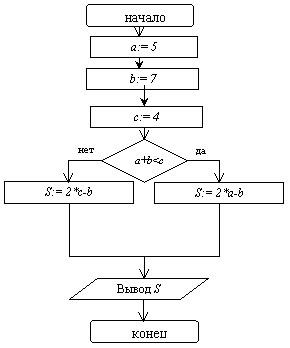 Алг zd1; Алг zd1;
a, b,с:цел;
S: вещ;
Нач
a:= 5,
b:= 7;
c :=4;
Если a+b<c, то
S:= 2*а- b
Иначе
S:= 2*с- b;
Кв;
Вывод S;
Кон.
Ответ: S= 1
Обратить внимание на оформление решения.
Задача 1. Найдите значение переменной S
после выполнения следующего алгоритма.
| |
a |
b |
c |
a+b<c |
S |
| 1. |
5 |
7 |
4 |
|
|
| 2. |
|
|
|
5+7<4 (нет) |
|
| 3. |
|
|
|
|
2*4-7 |
| 4. |
|
|
|
|
1 |
Ответ: S= 1
4. Закрепление.
Задания ля самостоятельного выполнения.
1 группа.
Задача. Найдите значение переменной S после
выполнения следующих алгоритмов.
3 группа.
Задача 1. Составьте алгоритм определения
максимального значения из трех заданных
различных переменных.
Задача 2. Составьте алгоритм, определяющий
является ли введенное число четным либо
нечетным.
Задача 3. Составьте алгоритм, определяющий
попадает ли точка А (X,Y) в окружность с радиусом R,
с центром в начале координат.
Рассмотреть решения задач №1, №3.
5. Итог урока.
Анализ, контроль, выставление оценок.
| 
