Цель урока:
- Актуализация знаний (повторение
изученного материала).
- Расширение кругозора, возбуждение
интереса к геометрии, к истории
математики.
- Развитие и закрепление теоретических и
практических навыков.
Приборы и материалы:
- Линейка.
- Циркуль.
- Карандаш.
- Альбомный лист.
- Алгоритм построения.
- Образцы чертежей.
- Портрет Л.Эйлера
Ход урока:
- Повторение (актуализация знаний).
- Мотивационный этап
- Изучение нового материала (получение
исторических знаний, построение
трисекции угла, построение окружности
Эйлера).
- Знакомство с жизнью и деятельностью
великого русского математика Леонарда
Эйлера.
На доске - портрет Л.Эйлера

I. Этап актуализации знаний (1мин)
Учитель:
Еще раз давайте вспомним, что такое
биссектриса, медиана и высота треугольника.
Закончите предложения:
Биссектриса-это…
Медиана-это…
Высота-это…
II. Мотивационный этап (3мин)
Учитель:
На предыдущих уроках мы с вами повторяли
задачи на построение биссектрис, высот,
медиан, построение треугольников, равных
данным и.т.д.
Любая ли задача решается с помощью
циркуля и линейки? Еще в древности
греческие математики встретились с тремя
задачами на построение, которые не
поддавались решению.
1. Задача об удвоении объема куба.
Требуется построить ребро куба, который
по объему был бы в два раза больше объема
данного куба.
2. Задача о трисекции угла.
Требуется произвольный угол разделить на
три равные части.
3. Задача о квадратуре круга.
Требуется построить квадрат, площадь
которого равнялась бы площади данного
круга.
Возникновение этих задач связано с целым
рядом легенд. Любопытна легенда, связанная
с первой задачей.
Царь Минос велел воздвигнуть памятник
сыну Главку. Архитекторы придали памятнику
форму куба, ребро которого равнялось 100
локтям. Но Минос нашел этот памятник
слишком малым и приказал удвоить объем.
Чувствуя свое бессилие в решении
поставленной задачи, архитекторы
обратились за помощью к ученым-геометрам,
но и те не смогли им помочь. Циркулем и
линейкой решить задачу нельзя.
III. Изучение нового материала (12мин*3)
1. Ученик (сообщение, выполнение чертежа)
Большое место задачам на построение
отводилось в " Началах Евклида", где
существование фигур, доказывается их
построением с помощью циркуля и линейки.
Немецкий ученый Карл Фридрих Гаусс
доказал тот факт, что точных методов для
деления окружности (дуги) на 7, 9, 11, 13, 14, 18, 21,
22, 23, 25 и еще много других частей нет. А вот на
три части мы сейчас попробуем разделить
дугу (угол). Это называется трисекцией.
Проведем трисекцию угла АОВ. Для
этого:
- Опишем дугу АВ с центром О и радиусом R.
- Проведем хорду АВ, т.О1 - середина
АВ
- Радиусом равным АО1 описываем
полуокружность
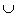 АnВ с центром О1
АnВ с центром О1
- Строим дугу
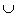 ВС,
стягивающую хорду ВС = АО1, ВС,
стягивающую хорду ВС = АО1, 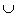 ВС
= 1/3 ВС
= 1/3 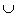 АnВ АnВ - Делим отрезок АВ на три равные части .BD=1/3АВ.
- Строим серединный перпендикуляр EY к
отрезку CD. Точка Y является пересечением
этого перпендикуляра с продолжением АВ
- Проводим радиусом DY дугу из точки Y.
Х- пересечение этой дуги с дугой 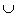 АmB.
АmB.
ВХ =1/3 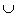 АmB , т.е.
АmB , т.е. 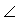 ВОХ
ВОХ 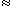
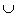 1/3 1/3
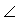 АОВ
АОВ
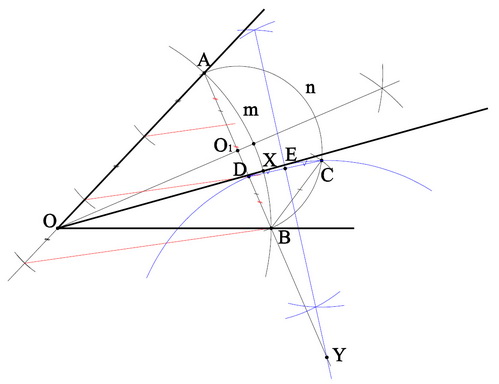
(ученики выполняют практическую
работу на построение трисекции угла вместе
с докладчиком-консультантом.) < Приложение
1 >
Учитель:
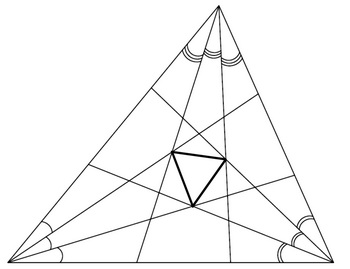
В 1904 году американский математик Ф.Морли
доказал, что если у каждой вершины провести
две трисектрисы, то точки пересечения
смежных трисектрис углов являются
вершинами равностороннего треугольника (показать
чертеж).
2-й Ученик (сообщение, выполнение
чертежа)
Первые упоминания о треугольнике мы
находим в Египетских папирусах, которым
более 4000 лет. Через 2000 лет появилась теорема
Пифагора и теорема Герона. В XV-XVI веках
появляется целый раздел, получивший
название " Новая геометрия треугольника"
Одна из замечательных теорем того времени
принадлежит Л.Эйлеру". Середины сторон
треугольника, основания его высот и
середины отрезков высот от вершины до точки
их пересечения, лежат на одной окружности.
"Эта окружность называется окружностью
Эйлера или окружностью 9 точек. Ее называют
так же окружностью Фейербаха, который
доказал, что эта окружность касается
окружности, вписанной в треугольник и всех
его не вписанных окружностей (т.е.
окружностей, касающихся одной из его сторон
и продолжений двух других). Свойства
окружности: rэ = 1/2 R
опис.окр. Центр окружности лежит на
середине отрезка, соединяющего центр
описанной окружности с точкой пересечения
высот.
Прямая, которой принадлежит этот отрезок,
называется прямой Эйлера. Этой прямой
принадлежит точка пересечения медиан.
Точки, симметричные ортоцентру (пересечение
высот) относительно оснований высот и
середин сторон лежат на описанной
окружности. Известно и множество других
свойств треугольника.
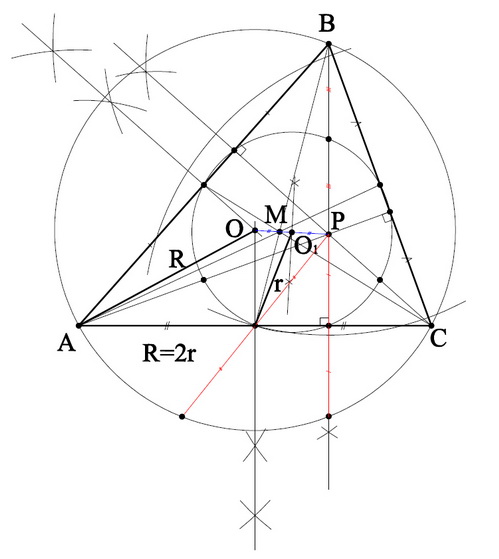
(ученики выполняют практическую работу
по построению окружности Эйлера вместе с
докладчиком-консультантом) < Приложение
1 >
Выше упомянутому Эйлеру принадлежит
огромное число открытий. Мы можем с
гордостью говорить об этом ученом, т.к. он
считался великим русским математиком.
Познакомимся с его биографией подробнее.
3-й Ученик (доклад по теме: "Жизнь и
деятельность Л.Эйлера") < Приложение
2 >
| 
