Ньютонова гора

Предоставим слово гениальному Ньютону, открывшему закон всемирного тяготения. В своих «Математических началах физики» он пишет (приводим это место ради облегчения понимания в вольном переводе):

«Брошенный камень под действием тяжести отклоняется от прямолинейного пути и падает на Землю, описывая кривую линию. Если бросить камень с большею скоростью, то он полетит дальше; поэтому может случиться, что он опишет дугу в десять, сто, тысячу миль и, наконец, выйдет за пределы Земли и не вернется на нее больше. Пусть AFB (рис. 1) представляет поверхность Земли, C — ее центр, a UD, UE, UF, UG — кривые линии, которые описывает тело, бросаемое в горизонтальном направлении с очень высокой горы со все большей и большей скоростью. Мы не принимаем во внимание противодействия атмосферы, т. е. предполагаем, что она совершенно отсутствует. При меньшой первоначальной скорости тело описывает кривую UD, при большей скорости — кривую UE, при еще больших скоростях — кривые UF, UG. При некоторой скорости тело обойдет вокруг всей Земли и возвратится к вершине горы, с которой его бросили. Так как при возвращении к исходному пункту скорость тела будет не меньше, чем в самом начале, то тело будет продолжать двигаться и дальше по той же кривой».

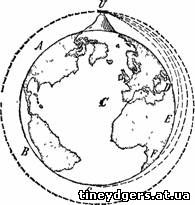
Рисунок 1. Как должны падать камни, бросаемые на вершине горы с огромной скоростью в горизонтальном направлении.

Если бы на этой воображаемой горе была пушка, то выброшенный ею снаряд при известной скорости никогда не упал бы обратно на Землю, а стал бы безостановочно кружиться вокруг земного шара. Путем довольно простого расчета нетрудно определить, что это должно наступить при скорости около 8 км в секунду. Другими словами, снаряд, выбрасываемый пушкой со скоростью восьми километров в секунду, навсегда покидает поверхность земного шара и становится спутником нашей планеты. Он будет мчаться в 17 раз быстрее, чем какая-либо точка на экваторе, и опишет полный оборот вокруг нашей планеты в 1 час 24 минуты. Если же сообщить снаряду большую скорость, он будет вращаться около Земли уже не по кругу, а по более или менее вытянутому эллипсу, удаляясь от Земли на огромное расстояние. При еще большей начальной скорости снаряд навсегда удалится от нашей планеты в мировое пространство. Это должно наступить при начальной скорости около 11 км в секунду. (Во всех этих рассуждениях имеются в виду снаряды, движущиеся в пустом пространстве, а не в воздушной среде.)

Теперь посмотрим, можно ли осуществить полет на Луну теми средствами, которые предлагал Жюль Верн. Современные пушки сообщают снарядам скорость не более двух километров в первую секунду. Это в пять раз меньше той скорости, с какой тело может полететь на Луну. Герои романа думали, что если они соорудят исполинскую пушку и зарядят ее огромным количеством взрывчатых веществ, им удастся получить скорость, достаточную, чтобы отправить снаряд на Луну.

Фантастическая пушка

И вот члены Пушечного клуба отливают гигантскую пушку, длиной в четверть километра, отвесно врытую в землю. Изготовляется соответственно огромный снаряд, который внутри представляет собою каюту для пассажиров. Вес его 8 тонн. Заряжают пушку хлопчатобумажным порохом — пироксилином — в количестве 160 тонн. В результате взрыва снаряд, если верить романисту, приобретает скорость в 16 км в секунду, но вследствие трения о воздух скорость эта уменьшается до 11 км в секунду. Таким образом, очутившись за пределами атмосферы, жюль-вернов снаряд обладает скоростью, достаточной, чтобы долететь до Луны.

Так описывается в романе. Что же может сказать об этом физика?

Проект Жюля Верна уязвим совсем не в том пункте, куда обычно направляется сомнение читателя. Во-первых, можно доказать (я доказываю это в книге «Межпланетные путешествия»), что пороховые пушки никогда не смогут сообщить снарядам скорости, большей 3 км в секунду.

Кроме того, Жюль Верн не посчитался с сопротивлением воздуха, которое при такой огромной скорости должно быть весьма велико и совершенно изменит картину полета. Но и помимо этого имеются серьезные возражения против проекта полета на Луну в артиллерийском снаряде.

Главные опасения вызывает участь самих пассажиров. Не думайте, что опасность грозит им во время полета от Земли до Луны. Если бы им удалось остаться живыми к тому моменту, когда они покинут жерло пушки, то во время дальнейшего путешествия им нечего уже было бы опасаться. Огромная скорость, с которой пассажиры будут мчаться в мировом пространстве вместе с их вагоном, столь же безвредна для них, как безвредна для нас, обитателей Земли, та еще большая скорость, с какой земной шар мчится вокруг Солнца.

Тяжелая шляпа

Самый опасный момент для наших путешественников представили бы те несколько сотых долей секунды, в течение которых каюта-снаряд движется в канале пушки. Ведь в течение этого ничтожно малого промежутка времени скорость, с какою пассажиры будут двигаться в пушке, должна возрасти от нуля до 16 км/сек! Недаром в романе пассажиры с таким трепетом ожидали выстрела. И Барбикен был вполне прав, утверждая, что момент, когда снаряд полетит, будет для пассажиров столь же опасен, как если бы они находились не внутри, а впереди снаряда. Действительно: в момент выстрела нижняя площадка каюты ударит пассажиров снизу с такой же силой, с какой налетел бы снаряд на всякое тело, находящееся на его пути. Герои романа отнеслись к этой опасности чересчур легко, воображая, что отделаются в худшем случае только приливом крови к голове…

Дело обстоит серьезнее. В канале ствола снаряд движется ускоренно: скорость его растет под постоянным напором газов, образующихся при взрыве. В течение ничтожной доли секунды скорость эта возрастает от 0 до 16 км/сек. Допустим для простоты, что возрастание скорости совершается равномерно; тогда ускорение, необходимое для того, чтобы в столь ничтожное время довести скорость снаряда до 16 км/сек, достигнет здесь круглым счетом 600 км в секунду за секунду (вычисления приведены далее на стр. 91–93).

Роковое значение этой цифры мы вполне поймем, если вспомним, что обычное ускорение силы тяжести на земной поверхности равняется всего 10 м в секунду за секунду. Отсюда следует, что каждый предмет внутри снаряда в момент выстрела оказывал бы на дно каюты давление, которое в 60 000 раз больше веса этого предмета. Другими словами: пассажиры чувствовали бы, что сделались словно в несколько десятков тысяч раз тяжелее! Под действием такой колоссальной тяжести они были бы мгновенно раздавлены. Один цилиндр мистера Барбикена весил бы в момент выстрела не менее 15 тонн (вес груженого вагона); такой шляпы более чем достаточно, чтобы раздавить ее владельца.

Правда, в романе описаны меры, принятые для ослабления удара: ядро снабжено пружинными буферами и двойным дном с водою, заполняющей пространство в нем. Продолжительность удара от этого немного растягивается, и следовательно, быстрота нарастания скорости ослабевает. Но при огромных силах, с которыми приходится здесь иметь дело, выгода от этих приспособлений получается мизерная. Сила, которая будет придавливать пассажиров к полу, уменьшается на ничтожную долю, — а не все ли равно, быть раздавленным шляпой в 15 или 14 тонн?!

Как ослабить сотрясение?

Механика дает указание на то, как можно было бы ослабить роковую быстроту нарастания скорости.

Этого можно достигнуть, если во много раз удлинить ствол пушки.

Удлинение потребуется, однако, весьма значительное, если мы хотим, чтобы в момент выстрела сила «искусственной» тяжести внутри снаряда равнялась обыкновенной тяжести на земном шаре. Приблизительный расчет показывает, что для этого нужно было бы изготовить пушку длиной ни мало, ни много, — в 6000 км! Другими словами, жюль-вернова «колумбиада» должна бы простираться в глубь земного шара до самого его центра… Тогда пассажиры могли бы быть избавлены от всяких неприятностей: к их обычному весу прибавился бы еще только такой же кажущийся вес вследствие медленного нарастания скорости, и они чувствовали бы, что стали всего вдвое тяжелее.

Впрочем, в течение краткого промежутка человеческий организм способен без вреда переносить увеличение тяжести в несколько раз. Когда мы скатываемся с ледяной горы вниз и здесь быстро меняем направление своего движения, вес наш в этот краткий миг заметно увеличивается, т. е. тело наше прижимается к санкам сильнее обычного. Увеличение тяжести раза в три переносится нами довольно благополучно. Если допустить, что человек может безвредно переносить в течение короткого времени даже десятикратное увеличение веса, то достаточно будет отлить пушку «всего» в 600 км длиною. Однако это мало утешительно, потому что и подобное сооружение лежит за пределами технически возможного.

Вот при каких лишь условиях мыслимо осуществление заманчивого проекта Жюля Верна: полететь на Луну в пушечном снаряде.

Для друзей математики

Среди читателей этой книги, без сомнения, найдутся и такие, которые пожелают сами проверить расчеты, упомянутые выше. Приводим здесь эти вычисления. Они верны лишь приблизительно, так как основаны на допущении, что в канале пушки снаряд движется равномерно-ускоренно (в действительности же возрастание скорости происходит неравномерно).

Для расчетов придется пользоваться следующими двумя формулами равномерно-ускоренного движения:

скорость v по истечении t-й секунды равна at, где а — ускорение:

v = at;

путь S, пройденный за t секунд, определяется формулой

S = at²/2.

По этим формулам определим прежде всего ускорение снаряда, когда он скользил в канале «колумбиады».

Из романа известна длина части пушки, не занятой зарядом, — 210 м; это и есть пройденный снарядом путь S.

Мы знаем и конечную скорость: v = 16 000 м/сек. Данные S и v позволяют определить величину t — продолжительность движения снаряда в канале орудия (рассматривая это движение как равномерно-ускоренное). В самом деле:

v = at = 16000,

откуда

t = 210/8000 = около 1/40 сек.

Снаряд, оказывается, скользил бы внутри пушки всего 1/40 секунды! Подставив

t = 1/40 в формулу v = at, имеем:

16 000 = 1/40 a, откуда a = 640 000 м/сек².

Значит, ускорение снаряда при движении в канале равно 640 000 м/сек², т. е. в 64 000 раз больше ускорения силы тяжести!

Какой же длины должна быть пушка, чтобы ускорение снаряда было всего в 10 раз больше ускорения падающего тела (т. е. равнялось бы 100 м/сек²)?

Это — задача, обратная той, которую мы сейчас решили. Данные:

a = 100 м/сек²,

v = 11 000 м/сек (при отсутствии сопротивления атмосферы такая скорость достаточна).

Из формулы v = at имеем:

11000 = 100t, откуда t = 110 сек.

Из формулы S = at²/2 = at×t/2 получаем, что длина пушки должна равняться

т. е. круглым счетом 600 км.