Интеллектуальная игра на тему «Умники и умницы» - МАТЕМАТИКА - ЗАНИМАТЕЛЬНЫЙ УРОК - РЕФЕРАТЫ

Эта игра может проводиться как внеклассное мероприятие между классами одной параллели. Участвовать в игре могут учащиеся 8 классов. Количество человек в команде не ограниченно – участниками игры могут быть все желающие.

Агонисты – по 3 участника от каждого класса.
Теоретики – ученики класса.
Заумник – ведущий – ученик 11 класса.
Эрудит – помощница ведущего – ученица 11 класса.
Высокий ареопаг – жюри в количестве трех человек, в состав которого входят три учителя математики.

1-й конкурс. "Пролог” (представление команд).
2-й конкурс. "Конкурс красноречия” (задания для команд).
3-й конкурс. "I этап”.
4-й конкурс. "II этап”.
5-й конкурс. "III этап”.
6-й конкурс. "Последний вопрос” (состязание теоретиков).
7-й конкурс. "Эпилог”.

Здравствуйте, уважаемые друзья! Сегодня мы проводим первую встречу в интеллект-шоу. "Умники и умницы”. Для участия в игре мы пригласили учащихся 8 классов.

За несколько дней до начала игры учащимся было предложено следующее задание.

Представьте, что вы – корреспондент газеты "Эрудит”. Ваша задача – написать краткую, яркую заметку на тему: "Докажите, что нужно изучать точные науки: математику, физику, информатику”.

Команде – участнице, набравшей наибольшее количество баллов за первый конкурс, предоставляется право выбора дорожки.

Напоминаем! Красная дорожка – нельзя ошибаться. Желтая дорожка – ошибиться можно только 1 раз. Зеленая дорожка – можно ошибиться два раза. Каждый агон начинается с зеленой дорожки. Время на обдумывание одного вопроса – 1 минута. Игра заканчивается в агоне, если один из участников дошел до рубежной черты. За победу команда получает 10 баллов. Если агонист не ответил на вопрос, то право ответа предоставляется теоретику любого класса, первому, кто поднял руку. За правильный ответ теоретик получает орден. Орден приравнивается к трем баллам.

После каждого агона проходит состязание теоретиков. Они отвечают на оставшиеся вопросы.

Право выбора дорожки в следующем этапе получает команда, имеющая наибольшее количество баллов в предыдущем этапе.

Наименьшее простое число (2)
Какой ученый создал руководство по математике под названием "Начала”? (Евклид)
Какое наибольшее число можно записать с помощью трех двоек? (2²²)
Как с точки зрения физики истолковать выражение "не подмажешь – не поедешь”? (Применение смазки в узлах механических устройств обуславливает уменьшение силы трения между трущимися деталями, поэтому облегчается их работа, уменьшаются износ деталей и расход топлива).
Найдите площадь квадрата, периметр которого равен 64 см. (256 см²).
Назовите имя французского математика, который ввел координатную плоскость. (Декарт).
Математическое предложение, не требующее доказательства. (Аксиома).
Как назывался счетный прибор, которым пользовались греки? (Абак).
Используя одно из геометрических свойств, определите какая из букв лишняя: Ф,Б,Ж? (Б не имеет ось симметрии).

Назовите самое геометрические направление в живописи. (Супрематизм или кубизм).
Автор первого русского учебника математики? (Магницкий).
В Египетской пирамиде на гробнице начертано число, которое делится без остатка на все числа от 1 до 10 включительно. Назовите это число. (2250).
В безветренную погоду футбольный мяч после удара футболиста летит вертикально вверх. Как соотносятся время подъема мяча и время падения? (Время падения мяча больше времени подъема).
Найдите длину окружности, если площадь круга равна 100 см². (20 см²)
Найдите площадь правильного треугольника со стороной 4 см. (4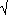3см²)
На какой угол поворачивается солдат по команде "кругом” (180⁰)
Математик, именем которого названа теорема, выражающая связь между корнями и коэффициентами квадратного уравнения. (Виет).
Чему равен периметр треугольника со сторонами 10см, 5см, 4 см. (Нет такого).

Как переводится слово "гипотенуза”? (Натянутая).
Назовите наименьшее трехзначное число, кратное 3, чтобы первой была цифра 7. (702).
Плот плывет по реке. В каком направлении от плота лодка с веслами быстрее удалится от него на одинаковое расстояние? (Во всех направлениях время удаления одинаково).
Чему равен оббьем 1 кг воды. (1 л.)
Единица измерения скорости на море. (Узел).
Число, которое не является ни отрицательным, ни положительным. (Нуль).
В какой стране впервые появились отрицательные числа? (Древний Китай).
В.Гюго заметил однажды, что разум человеческий владеет тремя ключами, позволяющими людям знать, думать, мечтать. Два из них – буква и нота. А каков третий ключ? (Цифра).
Что есть общего у равнобедренного треугольника и у степени? (Основание).

В каком треугольнике все высот пересекаются в одной вершине? (Прямоугольном).
Теорема о несправедливом делении: одному – все, а другому половину. (Катет прямоугольного треугольника, лежащий против угла в 30⁰, равен половине гипотенузы).
Какой угол опишет минутная стрелка за 5 минут? (30⁰)
Как называется многоугольник, у которого все стороны и углы равны? (Правильный).
Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны? (Медиана).
Как называется два числа, произведение которых равно 1? (Взаимно обратные).
Другое название независимой переменной? (Аргумент).
Кратчайшее расстояние от точки до прямой? (Перпендикуляр).
Назовите мельчайшую частицу данного вещества. (Молекула).

Подведение итогов. Команда-победительница определяется по наибольшему количеству полученных баллов. Интервью лучшего игрока.


	Т И Н Е Й Д Ж Е Р Ы Для тех, кто учится и учит
Главная Мой профиль Выход Вы вошли как Гость \| Группа "Гости" \| RSS
Четверг, 21.11.2024, 15:05:45