Цели:

Оборудование:

Ход урока

1. Орг. момент

– Здравствуйте ребята! Сегодня нам предстоит познакомиться с таким свойством предметов, которым обладает все, кто есть на свете. Как вы думаете, что это за свойство? (Предположения детей).

– А скоро мы это узнаем. Проверьте свою готовность к уроку.

– Какие геометрические фигуры вы видите на доске?

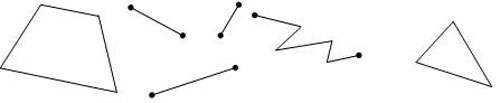
Рисунок 1

2. Изучение нового.

– На какие группы их можно разбить? (Отрезки и ломаные, замкнутые и незамкнутые)

Сегодня на уроке нам понадобятся отрезки. (У учителя и учеников на партах по 3 полоски разного цвета. Две из них имеют одинаковую длину, а третья – нет. Например, красная и синяя полоски по 15 см, а зеленая – 18 см)

а) Понятие величины. Непосредственное измерение длин отрезков

– Какие свойства предметов вы знаете? (Цвет, форма, размер, назначение и т.д.)

– Мы начинаем изучать такие свойства предметов, которые можно сравнивать с помощью знаков «больше», «меньше», «равно». Такие свойства называются величинами.

б) Опосредованное сравнение длин отрезков с помощью мерки

– Скажите, можем ли мы определить, какой цвет больше: красный или синий? Зеленый или желтый? (нет)

– Значит цвет нас сегодня не будет интересовать, цвет не является величиной. А можно ли сказать, чье назначение меньше – книжки или дерева? (нет)

– Является ли величиной назначение предметов? (тоже нет)

– Придумайте примеры таких свойств предметов, которые являются величиной (Пусть дети пофантазируют. Они могут назвать «размер», «рост», «температура» и т.д. Возможно, кто-нибудь из них назовет «длину».)

– Посмотрим, является ли величиной длина предметов. Попробуйте сравнить по длине полоски, которые лежат у вас на партах. Какая из них самая длинная? (Зеленая)

– Как это доказать? Мне почему-то кажется, что красная полоска длиннее. (Полоски надо положить друг на друга)

– Можно ли наложить их так: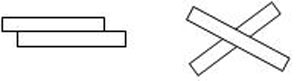

Рисунок 2

(Нет, надо подравнять концы).

– Кто из ребят мне покажет? (Один ученик сравнивает полоски у доски, а остальные выполняют у себя на партах. Выясняют, что красная и синяя полоски имеют одинаковую длину, а зеленая полоска – длиннее. Записывают: з > к, с < з, к = с)

– Итак, мы убедились, что длины полосок можно сравнить с помощью знаков >, < или =. Значит, длина является величиной.

(В разных концах доски нарисованы отрезки a = 80 см и b = 90 см, так что явно не видно, какой из них длиннее, у детей карточки с изображением отрезков, отрезок a = 8 см, b = 9 см)

– У каждого из вас есть карточка

– Что на ней изображено? (отрезки)

– Посмотрите, на доске такие же отрезки, только немного увеличенные.

– Ребята, как узнать, какой из этих отрезков длиннее? Как это доказать? (После обсуждения вариантов, предложенных детьми, учитель подводит их к мысли об использовании мерки).

– Может быть, нам поможет наша красная полоса? (Дети должны догадаться, что нужно определить, сколько раз эта полоска отложится в каждом отрезке, а затем сравнить полученные числа).

– Ребята, вы должны очень аккуратно и точно измерить оба отрезка, проговаривая при этом, что вы делаете.

– Посмотрите, как это делаю я. (Учитель показывает на одном из отрезков).

– От одного из концов отрезка откладываем мерку, там, где мерка закончилась, делаем отметку; от полученной отметки откладываем мерку еще раз, потом еще раз до тех пор пока отрезок не закончится.

– Всем все понятно? Кто что-то не понял – поднимите руки (Дети измеряют отрезки).

– Сколько раз отложилась красная полоска (мерка) в отрезка a (5 раз). Значит, а = 5 к.

– А в отрезке b сколько раз отложилось (6 раз) – значит b = 6 к.

– Какой из этого мы можем сделать вывод? (a < b, т.к. 5 < 6).

– Таким образом, с помощью измерений сравнение длин отрезков свелось к сравнению чисел.

в) Необходимость использования при сравнении отрезков одинаковой мерки

– У вас на столах есть еще одна мерка зеленого цвета. Попробуйте измерить отрезок b этой меркой, а отрезок a меркой красного цвета. (Дети выполняют измерение, а учитель выполняет его у доски).

– Сколько мерок красного цвета укладываются в отрезке a (a = 5 к).

– Сколько мерок зеленого цвета укладывается в отрезке b (b = 5 з).

– В отрезке a пять мерок (полосок) и в отрезке b тоже 5 мерок (полос).

– Значит, мы какой можем сделать вывод (a=b).

– А мы только что получили, что a < b. Где же ошибка? (Причиной ошибки является использование разных мерок)

Так к какому открытию мы сегодня пришли? (Сравнивать отрезки можно только тогда, когда они измерены одинаковыми мерками).

Для закрепления этого вывода можно предложить практическую работу в тетрадях: поставить точку и через десять клеток еще одну точку. Соединить их.

Миша говорит, что длина отрезка равна десяти, Коля – 5, Вася – 2. Почему у них такие разные ответы? (Численные значение величины зависит от мерки )

– Как вы думаете, а выбор мерки имеет значение при выяснении равенства или неравенства длин отрезков? (Предположения детей).

– Давайте проверим.

– Сколько раз зеленая мерка откладывается в отрезке a? (4 раза).

– А в отрезке b? (5 раз).

– Значит, измеряя отрезки зеленой меркой что мы получили? (a < b, т.к. 4 < 5).

– Какой вывод сделаем? (Выбор мерки не имеет значения)

– Ребята, а сейчас я вам сообщу что-то очень важное, будьте внимательны: Мерка – с помощью которой измеряют длины отрезков называется единичным отрезком или единицей измерения.

– Какие единичные отрезки мы использовали? (мерки разного цвета)

– Вспомните, как измеряли длину удава в сказке Г. Остера? (в попугаях, удав был длиной 38 попугаев)

г) Первые единицы длины. Сантиметр.

– Ребята, а как вы думаете, как древние люди измеряли длину? (ответы детей)

В древности использовались для измерения длин те измерительные приборы, которые всегда были при себе. Одним из самых распространенных единиц длины был локоть, т.е. расстояние от локтя до конца среднего пальца (показ). Локтями купцы измеряли продаваемые ткани, наматывая их на руку, высоту дерева, срубленного на постройку дома и т.д.

– Сейчас мы с вами воспользуемся одной древних мерок.

(Учитель вызывает к доске 3 человека)

– Вася, какова длина класса? (19 шагов)

Ребята, чем можно измерить длину класса? (шагами)

(Дети шагами измеряют длину, получая разное количество шагов)

– Так сколько шагов длина нашего класса? (На этот вопрос нельзя точно ответить, потому что у всех разные шаги)

– Ребята, а чем удобно измерить длину парты? (ладонью).

(Дети измеряют длину парты ладонями)

– Так сколько ладоней длина парты? (у всех разные ответы).

– На этот вопрос нельзя точно ответить, потому что у всех ладони разные.

– У каждого на парте лежит тесьма. Какой из древних мерок можно воспользоваться, чтобы измерить длину тесьмы? (локтем)

– Чему равна длина тесьмы? (У всех разные ответы) Учитель берет эти тесемки и показывает с помощью приложения, что они равны.

– Почему же у всех разные ответы? (Потому что длины локтя у всех разные)

– Как же быть, если у каждого свой вариант ответа? (предложения детей) (возможно, кто-нибудь из детей догадается что нужна единая мерка, признанная всеми) Если нет, то учитель сообщает сам.

Чтобы не ошибаться, используют общие для всех стран единицы измерения. Одной из них является сантиметры (на доске показывается карточка: сантиметр).

Дается сокращенная запись – см.

(У детей на партах лежат полоски длиною 1 см. – желтого цвета).

– Возьмите желтую мерку – это и есть 1 см (Дети рассматривают).

– Положите полоску на лист тетради. Сколько клеток она занимает (2 клетки).

– Положите полоску на линейку.

3. Закрепление

Сколько сантиметров укладывается в верхней полоске? (4 см) Сколько сантиметров в нижней полоске? (10 см)

– Значит какой вывод мы можем сделать?

– Измерьте фиолетовый отрезок с помощью красной мерки. Какой сделаем вывод?

(Далее можно организовать работу в группах. Первый ряд измеряет длину карандаша, второй – длину отвертки, третий – длину болта)

4. Итог

– Ребята, с чем вы сегодня познакомились? (С величиной)

– Что называется величиной? (Величина – это то, что может быть измерено и результат измерения выражен числом)

– С какой величиной мы познакомились сегодня? (С длиной)

– Что нужно сделать, чтобы измерить величину (длину)? (Чтобы измерить величину надо выбрать мерку и узнать сколько раз она содержится в измеряемой величине)

– А при сравнении двух отрезков можно пользоваться разными мерками, например, первый отрезок измерим с помощью зеленой мерки, а второй с помощью желтой мерки? (Если изменяется мерка, то изменяется и значение величины. Поэтому сравнивать величины можно только тогда когда они измерены одной и той же меркой)

– Какие единицы измерения длины использовались в древности?

– Почему отказались от древних единиц измерения? (единицы измерения длины, которые использовались в древности, были неточными, т.к. зависели от размеров тела измеряющего)

– В наше время и во всех странах какие единицы измерения используются? (сейчас используют единые для всех стран единицы измерения длины. Одной из них является сантиметр)

5. Домашнее задание

1) Придумать примеры величин.

2) Сравнить длину и ширину какого-нибудь стола (письменного, обеденного) с помощью красной мерки. Сделать записи.

3) Измерить длину подоконника сначала красной, а затем зеленой мерками. Сделать выводы.