Помимо рассмотренных нами логических операций ограничения, обобщения, определения и деления понятия, существуют еще две важные операции. Это сложение и умножение понятий.

Сложение понятий – это логическая операция объединения двух и более понятий, в результате которой образуется новое понятие с объемом, охватывающим собой все элементы объемов исходных понятий. Например, при сложении понятий школьник (Ш) и спортсмен (С) образуется новое понятие, в объем которого входят как все школьники, так и все спортсмены. Результат сложения понятий, часто называемый логической суммой, на схеме Эйлера изображается штриховкой (рис. 15).

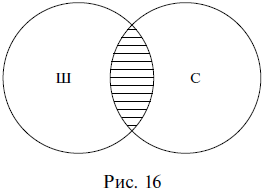
Умножение понятий – это логическая операция объединения двух и более понятий, в результате которой образуется новое понятие с объемом, охватывающим собой только совпадающие элементы объемов исходных понятий. Например, при умножении понятий школьник (Ш) и спортсмен (С) образуется новое понятие, в объем которого входят только школьники, являющиеся спортсменами, и спортсмены, являющиеся школьниками. Результат умножения понятий, часто называемый логическим произведением, на схеме Эйлера изображается штриховкой (рис. 16).

Мы привели примеры сложения и умножения понятий, которые находятся между собой в отношении пересечения: школьник и спортсмен. При других отношениях между понятиями результаты сложения и умножения (логическая сумма и логическое произведение), разумеется, будут иными. Результаты сложения понятий, при сравнении их с результатами умножения, полностью совпадают только в случае равнозначности, частично совпадают в пересечении и совершенно не совпадают в соподчинении, противоположности и противоречии (в этих трех случаях результатом умножения является нулевое или пустое понятие). В отношении подчинения результатом сложения является родовое понятие, а результатом умножения – видовое.

Как правило, в естественном языке (том, на котором мы общаемся) результат сложения понятий выражается союзом ИЛИ, а умножения – союзом И. В результате сложения понятий школьник и спортсмен образуется новое понятие, в объем которого входит любой человек, если он является ИЛИ школьником, ИЛИ спортсменом, а в результате умножения этих понятий в объем нового понятия входит любой человек, если он является И школьником, И спортсменом одновременно.

О возможных разночтениях при употреблении союзов ИЛИ и ИВ. И. Свинцов пишет: «Что касается союзов ИЛИ и И, то нужно отметить их многозначность, способную в известных ситуациях создавать достаточно неопределенное представление о характере связи между некоторыми исходными понятиями. Удачна ли, например, следующая формулировка одного из правил пользования городским транспортом: Безбилетный проезд и бесплатный провоз багажа наказываются штрафом! Представим себе два подмножества, которые могут быть выделены во множестве пассажиров-нарушителей. В одно из них войдут пассажиры, не взявшие билеты, в другое – не оплатившие провоз багажа.

Если союз И рассматривать как показатель логического умножения, то придется признать, что штраф должен быть наложен только на тех пассажиров, которые совершили сразу два проступка (но не какой-то один из них). Разумеется, житейский смысл ситуации, предусмотренной данным правилом, настолько ясен, что всякие разночтения этой формулировки, вероятно, были бы признаны казуистикой, но все же использование союза ИЛИ здесь следует признать предпочтительным».

Однако следует отметить, что и в данном случае из-за неоднозначности разделительного союза ИЛИ могут возникнуть недоразумения. Дело в том, что этот союз может употребляться в нестрогом (неисключающем) значении и в строгом (исключающем). Например, в высказывании Можно изучать английский язык или немецкий союз ИЛИ употребляется в нестрогом значении, так как можно изучать и тот, и другой язык одновременно, одно другого не исключает. В данном случае разделительный союз ИЛИ очень близок к соединительному союзу И. С другой стороны, в высказывании Он родился в 1987 году или в 1989 году союз ИЛИ употребляется в строгом значении, так как если он родился в 1987 году, то никак не в 1989 году, и наоборот, два варианта здесь друг друга исключают. (О различных значениях союза ИЛИ мы еще будем говорить далее.)

Если в рассмотренное выше правило пользования городским транспортом поставить союз ИЛИ вместо союза И, как предлагает В. И. Свинцов, то получится следующее: Безбилетный проезд или бесплатный провоз багажа наказываются штрафом. В данном случае союз ИЛИ, являясь показателем логического сложения, должен восприниматься в его нестрогом, неисключающем значении. Но ведь в указанной фразе этот союз можно истолковать и в строгом, исключающем значении. Тогда получится, что штраф накладывается или только на тех пассажиров, которые не оплатили проезд, или же только на тех, которые бесплатно провозят багаж. Правда, в этом случае не совсем понятно, кто же наказывается штрафом – те или другие. Поразмыслив, можно прийти к выводу, что штрафу подвергаются то те, то другие – на усмотрение контролера и в зависимости от ситуации.

В силу всего сказанного надо отметить, что употребление союза ИЛИ всякий раз нуждается в комментарии относительно того, в строгом или нестрогом значении он используется. Понятно, что без этого комментария вполне возможны различного рода недоразумения. Поэтому нередко употребляется своеобразный союз-гибрид ИЛИ/И, указывающий на то, что союз ИЛИ используется в некоем тексте в его нестрогом значении. Таким образом, наиболее целесообразно сформулировать правило оплаты проезда в городском пассажирском транспорте следующим образом: Безбилетный проезд или/и бесплатный провоз багажа наказываются штрафом. В данной, может быть, не совсем удобной, с точки зрения языка, формулировке все возможные разночтения и недоразумения исключаются.