Терминами суждения называются его субъект и предикат.

Термин считается распределенным (развернутым, исчерпанным, взятым в полном объеме), если в суждении речь идет обо всех объектах, входящих в объем этого термина. Распределенный термин обозначается знаком «+», а на схемах Эйлера изображается полным кругом (кругом, который не содержит в себе другого круга и не пересекается с другим кругом) (рис. 22).

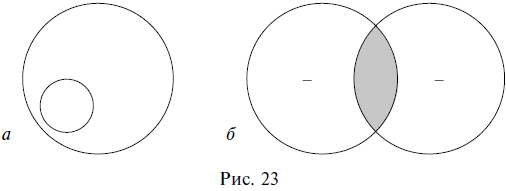
Термин считается нераспределенным (неразвернутым, неисчерпанным, взятым не в полном объеме), если в суждении речь идет не обо всех объектах, входящих в объем этого термина. Нераспределенный термин обозначается знаком «—», а на схемах Эйлера изображается неполным кругом (кругом, который содержит в себе другой круг (рис. 23а) или пересекается с другим кругом (рис. 23б).

Например, в суждении Все акулы (S) являются хищниками (Р) речь идет обо всех акулах, значит, субъект этого суждения распределен. Однако в данном суждении речь идет не обо всех хищниках, а только о части хищников (именно о тех, которые являются акулами), следовательно, предикат указанного суждения нераспределен. Изобразив отношения между субъектом и предикатом (которые находятся в отношении подчинения) рассмотренного суждения схемами Эйлера, увидим, что распределенному термину (субъекту акулы) соответствует полный круг, а нераспределенному (предикату хищники) – неполный (попадающий в него круг субъекта как бы вырезает из него какую-то часть) (рис. 24).

Распределенность терминов в простых суждениях может быть различной в зависимости от вида суждения и характера отношений между его субъектом и предикатом.

Проще всего устанавливать распределенность терминов в простых суждениях с помощью схем Эйлера. Достаточно уметь определять вид отношений между субъектом и предикатом в предложенном суждении и изображать их круговыми схемами. Далее еще проще – полный круг, как уже говорилось, соответствует распределенному термину, а неполный – нераспределенному. Например, требуется установить распределенность терминов в суждении Некоторые русские писатели – это всемирно известные люди. Сначала найдем в этом суждении субъект и предикат: русские писатели – субъект, всемирно известные люди – предикат. Теперь установим, в каком отношении они находятся. Русский писатель может как быть, так и не быть всемирно известным человеком, и всемирно известный человек может как быть, так и не быть русским писателем, следовательно, субъект и предикат указанного суждения находятся в отношении пересечения. Изобразим это отношение на схеме Эйлера, заштриховав ту часть, о которой идет речь в суждении (рис. 25).

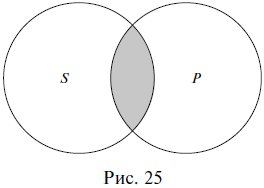И субъект, и предикат изображаются неполными кругами (у каждого из них как бы отрезана какая-то часть), следовательно, оба термина предложенного суждения нераспределены (S —, Р —).

Рассмотрим еще один пример. Надо установить распределенность терминов в суждении Некоторые люди – это спортсмены. Найдя в этом суждении субъект и предикат (люди – субъект, спортсмены – предикат) и установив отношение между ними (подчинение), изобразим его на схеме Эйлера, заштриховав ту часть, о которой идет речь в суждении (рис. 26).

Круг, обозначающий предикат, является полным, а круг, соответствующий субъекту, – неполным (круг предиката как бы вырезает из него какую-то часть). Таким образом, в данном суждении субъект нераспределен, а предикат распределен (S —, Р +).