1. Из первого мешка надо вытащить одну
монету, из второго – две, из третьего – три, и т. д. (из десятого мешка –
все 10 монет). Далее следует один раз взвесить все эти монеты вместе.
Если бы среди них не было фальшивых монет, т. е. все они были бы весом
по 10 граммов, то общий их вес составил бы 550 граммов. Но поскольку
среди взвешиваемых монет есть фальшивые (по 11 граммов), то их общий вес
будет больше 550 граммов. Причем, если он окажется 551 грамм, то
фальшивые монеты находятся в первом мешке, ведь из него мы взяли одну
монету, которая и дала один лишний грамм. Если общий вес будет 552
грамма, значит, фальшивые монеты находятся во втором мешке, ведь из него
мы взяли две монеты. Если общий вес будет 553 грамма, значит, фальшивые
монеты находятся в третьем мешке, и т. д. Таким образом с помощью
только одного взвешивания можно точно установить, в каком мешке
находятся фальшивые монеты.
2. Надо взять печенье из банки с надписью
«Овсяное печенье» (можно из любой другой). Так как банка надписана
неправильно, то это будет песочное печенье или шоколадное. Допустим, вы
достали песочное. После этого надо поменять местами этикетки «Овсяное
печенье» и «Песочное печенье». А поскольку по условию все этикетки
перепутаны, то теперь в банке с надписью «Шоколадное печенье» находится
овсяное, а в банке с надписью «Овсяное печенье» находится шоколадное,
значит, надо поменять местами и эти две этикетки.
3. Из шкафа нужно достать только три носка.
При этом возможно всего 4 варианта: все три носка белые; все три носка
черные; два носка белые, один черный; два носка черные, один белый. В
каждой из этих комбинаций имеется одна совпадающая пара – белая или
черная.
4. Часы пробьют 12 часов за 66 секунд. Когда
часы бьют 6 часов, то от первого удара до последнего проходит 5
интервалов. Интервал составляет 6 секунд (1/5 часть от 30). Когда часы
бьют 12 часов, то от первого удара до последнего проходит 11 интервалов.
Так как длина интервала равна 6 секундам, то, для того чтобы пробить 12
часов, часам требуется 66 секунд: 11 · 6 = 66.
5. Пруд будет покрыт листьями лилии
наполовину на 99-й день. По условию число листьев каждый день
удваивается, и если на 99-й день пруд покрыт листьями наполовину, то на
следующий день и вторая половина пруда будет покрыта листьями лилии,
т. е. полностью пруд покроется ими через 100 дней.
6. Путь, пройденный на пятый этаж (4 пролета)
пассажирским лифтом, вдвое больше пути, пройденного на третий этаж (2
пролета) грузовым. Поскольку пассажирский лифт идет в 2 раза быстрее,
чем грузовой, то они пройдут свои пути одновременно.
7. Для решения этой задачи надо составить уравнение. Количество гусей в стае – это х. «Вот если бы нас было столько, сколько сейчас (т. е. х), – сказали гуси, – да еще столько (т. е. х), да еще пол-столько (т. е. 1/2х), да еще четверть-столько (т. е. 1/4х), да еще ты (т. е. 1 гусь), вот тогда нас было бы 100 гусей». Получается следующее уравнение: Произведем сложение в левой части равенства: Итак, в стае было 36 гусей.
8. Ошибка заключается в возведении каждой
части равенства —2 = 2 в квадрат. Создается видимость, что над каждой
частью равенства совершается одна и та же операция (возведение в
квадрат), на самом же деле над каждой частью равенства совершаются
различные операции, ведь левую часть мы умножаем на —2, а правую
умножаем на 2.
9. Утверждение, что атомное ядро меньше самого атома в 2 раза, конечно же, неверно: ведь 10-12 см меньше, чем 10-6 см не в 2 раза, а в миллион раз.
10. Самолет в полете «держится» на воздухе, поэтому долететь на самолете до Луны невозможно, ведь воздуха в открытом космосе нет.
11. Иголка сделана из стали, а монета из
меди. Сталь намного тверже меди, и поэтому иголкой вполне можно
проколоть монету. Только вручную это сделать невозможно. Если же
попытаться забить иголку в монету молотком, то тоже ничего не получится:
площадь острого конца иголки настолько мала, что ее кончик будет,
вибрируя, скользить по поверхности монеты. Чтобы иголка была устойчивой,
надо вбить ее молотком в монету через кусок мыла, парафина или дерева:
этот материал придаст иголке неизменное и нужное направление, и в этом
случае она свободно пройдет через медную монету.
12. В стакан можно поместить более тысячи
булавок. В этом случае ни капли воды из него не выльется, но над краями
стакана образуется небольшая водяная выпуклость, «горка». По закону
Архимеда тело, погруженное в воду, вытесняет объем воды, равный объему
тела. Объем одной булавки настолько мал, что объем водяной «горки» над
поверхностью стакана равен объему более тысячи булавок.
13. На портрете изображен сын Иванова. Для решения задачи можно составить простую схему: 14. Надо
обратиться к любому из воинов со следующим вопросом: «Если я спрошу
тебя, этот ли выход ведет на свободу, то ты ответишь мне „да"?» При
такой постановке вопроса тот воин, который все время лжет, будет
вынужден говорить правду. Допустим, вы, показывая ему на выход к
свободе, говорите: «Если я спрошу тебя, этот ли выход ведет на свободу,
то ты ответишь мне „да"?» Правдой в этом случае будет, если он ответит
«нет», но ему ведь надо солгать и поэтому он вынужден сказать «да».
15. Вор нижние концы веревок связал вместе.
По одной из них он полез к потолку, обрезал вторую веревку на расстоянии
примерно 30 сантиметров от потолка и позволил ей упасть вниз. Из куска
второй веревки, оставшегося висеть, он связал петлю. Затем, ухватившись
за петлю, он перерезал первую веревку и просунул ее в петлю.
После этого он спустился по двойной веревке вниз и вытащил веревку из петли.
16. Если таксист глух, как он понял, куда везти девушку? И еще: как он понял, что она вообще что-то говорит?
17. Вода никогда не достигнет иллюминатора, потому что лайнер поднимается вместе с водой.
18. Он рассуждал так: «Каждый из нас может
думать, что его собственное лицо чистое. Б. уверен, что его лицо чистое,
и смеется над испачканным лбом В. Но если бы Б. видел, что мое лицо
чистое, он был бы удивлен смеху В., так как в этом случае у В. не было
бы повода для смеха. Однако Б. не удивлен, значит, он может думать, что
В. смеется надо мной. Следовательно, мое лицо испачкано».
19. Нужно сдвинуть верхнюю спичку, образовав крохотный квадрат в центре фигуры.
20. Точка на тропинке, которую путешественник
проходит в одно и то же время суток как во время подъема, так и во
время спуска, существует (А). В этом легко убедиться с помощью следующей схемы (рис. 53). Ось х – это время суток, а ось у – это
высота подъема. Кривые линии – это графики подъема и спуска
соответственно. Точка их пересечения – как раз та самая, которую
проходит путешественник в одно и то же время суток и на подъеме, и на
спуске.
21. Статуи надо расположить следующим образом (рис. 54). 22. См. рис. 55. 23. Обмен
выгоден математику и невыгоден торговцу, так как количество денег,
которые выплачивает торговец математику, пусть даже ничтожно малое
вначале, увеличивается в геометрической прогрессии, а деньги, которые
платит математик торговцу, увеличиваются в арифметической прогрессии.
Через 30 дней математик отдаст торговцу около 50 000 рублей, а торговец
будет должен математику более 10 000 000 рублей.
24. Новый год и раньше (т. е. по старому
стилю) встречали 1 января. Однако старое 1 января (старый Новый год)
сейчас, т. е. по новому стилю, попадает на 14 января, поэтому никакого
противоречия и недоразумения здесь нет. В условии задачи создается
видимость противоречия за счет того, что в одних и тех же словах
смешиваются различные понятия: Новый год по новому стилю и Новый год по
старому стилю. И действительно, Новый год по новому стилю в старом стиле
приходился бы на 19 декабря, а Новый год по старому стилю в новом стиле
приходится на 14 января.
25. См. рис. 56. 26. См. рис. 57. 27. Человек,
который стоит слева, будь он Правдолюбом, на вопрос «Кто стоит рядом с
тобой?» не мог бы ответить то, что ответил – «Правдолюб». Значит, слева
не Правдолюб.
Но Правдолюб и не в центре, так как, будучи Правдолюбом,
на поставленный вопрос «Кто ты?» он не мог бы ответить так, как ответил
– «Дипломат».
Значит, Правдолюб стоит справа, и, следовательно, рядом с ним, т. е. в центре, находится Лжец, а слева стоит Дипломат.
28. Последовательность переливаний
представлена в следующей таблице, где I – ведро объемом 10 литров; II –
ведро объемом 7 литров; III – ведро объемом 3 литра. Таким
образом, разделить 10 литров вина пополам, используя два пустых ведра
объемом 7 литров и 3 литра, можно с помощью 10 переливаний.
29. Катя придет к поезду первой, а Андрей,
скорее всего, опоздает на поезд, так как он придет на вокзал к тому
времени, когда на его часах будет 8 часов 05 минут. А на самом деле
будет на 10 минут позже – в 8 часов 15 минут. Катя постарается прийти по
своим часам к 7 часам 50 минутам, а на самом деле тогда будет 7 часов
45 минут.
30. Для решения этой задачи надо составить
уравнение. Но сначала на основе запутанного ответа динозавра следует
построить следующую схему (возраст черепахи в прошлом примем за х): Итак,
на схеме видим, что сейчас динозавру действительно в 10 раз больше лет,
чем было черепахе тогда, когда динозавру было столько лет, сколько
черепахе сейчас. Поскольку разница в возрасте и в прошлом, и в настоящем
остается одинаковой, составим уравнение 110 – х = 10х – 110.
Преобразуем его:
110 + 110 = 10х + х,
220 = 11х,
х = 220: 11 = 20.
Следовательно, черепахе в прошлом было 20 лет, динозавру сейчас в 10 раз больше, т. е. 200 лет.
31. Сумма диаметров малых полуокружностей (АС) + (CD) + (DB) равна диаметру большой полуокружности АВ, но ввиду того, что длина полуокружности равна половине произведения числа π
на диаметр, пройденные автомобилями расстояния будут совершенно
одинаковыми. Следовательно, отставание милицейского автомобиля от
угонщика не уменьшится, и погоня на этом участке не увенчается успехом.
32. Для решения этой задачи надо составить простую схему (обозначим нынешний возраст Кати как х): Из схемы следует, что самая старшая – Катя, далее следуют по возрасту Оля и Настя.
33. Все правдивые верно утверждали, что все
написанное – правда, но и все лжецы ложно утверждали, что все написанное
ими – правда. Таким образом, все 35 сочинений оказались с утверждением о
правдивости написанного.
34. У каждого человека 2 родителя, 4 бабушки и
дедушки, 8 прабабушек и прадедушек, 16 прапрабабушек и прапрадедушек.
Узнаем, сколько было прапрабабушек и прапрадедушек у всех прапрабабушек и
прапрадедушек каждого из нас: 16 · 16 = 256. Этот результат получается,
конечно же, если исключить случаи кровосмешения, т. е. браки между
различными родственниками.
Если принять в расчет, что одно поколение – это примерно
25 лет, то восемь поколений (о которых шла речь в условии задачи)
соответствуют 200 годам, т. е. 200 лет назад каждые 256 человек на Земле
были родственниками каждого из нас. За 400 лет число наших предков
составит: 256 · 256 = 65 536 человек, т. е. 400 лет назад у каждого из
нас было 65 536 живущих на планете родственников. Если же «открутить»
историю на 1000 лет назад, то получится, что все население Земли того
времени являлось родственниками каждому из нас. Значит, действительно
все люди – братья.
35. Можно попытаться, используя инерцию бутылки, резким движением выдернуть платок из-под нее.
Но, скорее всего, ничего не получится: положение бутылки
слишком неустойчиво. Однако вспомним, что сила трения уменьшается при
вибрациях. Кулаком одной руки надо равномерно и несильно стучать по
столу недалеко от бутылки, а другой рукой – аккуратно тянуть платок. При
определенной частоте и силе ударов по столу платок начнет плавно
выскальзывать из-под бутылки. При этом важно обратить внимание на то,
чтобы у края платка была не очень большая кромка: она, как правило,
сбивает бутылку в последний момент. Поэтому лучше, чтобы платок вообще
был без кромки.
36. С помощью единственной черточки один из знаков плюс превратится в цифру четыре, в результате чего получается равенство:
545 + 5 = 550.
Вот эта черточка: → 5'+ 5 + 5 = 550.
37. В этом рассуждении в одних и тех же
словах смешиваются различные математические операции: деление на два и
умножение на два. На этом смешении и основан подвох в виде внешне
правильного доказательства ложной мысли.
38. См. рис. 58. 39. Номер для квартиры.
40. Нельзя, так как через 72 часа, т. е.
через трое суток, будет опять 12 часов ночи, а солнце ночью не светит
(если, конечно, дело не происходит за Полярным кругом в полярный день).
41. У хозяйки 25 рублей, у мальчика 2 рубля.
Всего 27 рублей, значит, те 2 рубля, которые получил мальчик, входят в
27 рублей. А в условии задачи к 27 рублям прибавлено 2 рубля, которые у
мальчика, и поэтому получается 29 рублей. Надо к 27 рублям не прибавлять
2 рубля, а отнимать.
42. 1 л равен 1 дм3. Следовательно, в бассейн налили 1 000 000 дм3 воды, или 1000 м3 воды (так как 1 м равен 10 дм). Зная площадь бассейна (1 га = 10 000 м2) и объем налитой в него воды, легко вычислить его глубину: В бассейне глубиной 10 сантиметров плавать невозможно.
43. Для сравнения указанных величин надо
привести квадратный корень и кубический к корню одной степени. Это может
быть корень шестой степени. Соответственно изменятся и подкоренные
выражения. Получится 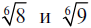 . Корень шестой степени из девяти немного больше такого же корня из восьми, следовательно, . Корень шестой степени из девяти немного больше такого же корня из восьми, следовательно, 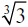 больше, чем больше, чем  . .
44. Обозначим стоимость линейки как х. Тогда у одного мальчика имеется денег (х – 24) копеек, а у другого (х – 2) копеек. При сложении своих денег они все равно не смогли купить линейку. Составим простое неравенство:
(x – 24) + (x – 2) < x.
Преобразуем его:
x – 24 + х – 2 < х,
2х – 26 < х,
2х – х < 26,
х < 26.
Итак, линейка стоит меньше 26 копеек, но больше 24
копеек, так как по условию у одного мальчика не хватает до ее стоимости
24 копеек. Линейка стоит 25 копеек.
45. Надо спросить любого депутата: «Вы
консерватор?» Если он ответил «да», то сегодня четное число, а если
«нет», то нечетное. По четным числам консерваторы скажут правдивое «да»,
а либералы, говоря неправду, тоже произнесут «да». По нечетным числам,
наоборот, консерваторы, отвечая на вопрос, скажут «нет», но либералы,
говорящие в эти дни только правду, тоже скажут «нет».
46. На первый взгляд кажется, что бутылка
стоит 1 рубль, а пробка – 10 копеек, но тогда бутылка дороже пробки на
90 копеек, а не на 1 рубль, как по условию. На самом деле, бутылка стоит
1 рубль 05 копеек, а пробка стоит 5 копеек.
47. Может показаться, что Оля проходит 30
ступенек – в 2 раза меньше, чем Катя (так как она живет в 2 раза ниже).
На самом деле это не так. Когда Катя поднимается на четвертый этаж, она
преодолевает 3 лестничных пролета между этажами. Значит, между двумя
этажами 20 ступенек: 60: 3 = 20. Оля поднимается с первого этажа на
второй, следовательно, она преодолевает 20 ступенек.
48. Это число 91, которое при переворачивании
вверх ногами превращается в 16. При этом оно уменьшается на 75
(поскольку 91–16 = 75). При решении этой задачи надо учитывать, что при
переворачивании числа его цифры не только переворачиваются, но и
меняются местами.
49. На развернутом листе будет 128 дырок. Надо принять во внимание, что при каждом складывании листа количество дырок удваивается.
50. Три человека: дед, отец и сын – это два отца и два сына – поймали трех зайцев, каждый по одному.
51. Эффект этой задачи-фокуса заключается в
том, что увеличение любого трехзначного числа до шестизначного путем его
дублирования равносильно умножению этого трехзначного числа на 1001.
Кроме того, произведение чисел 13, 11 и 7 также равно 1001.
Следовательно, если получившееся шестизначное число разделить в любой
последовательности на эти три числа (13, 11, 7), то получится исходное
трехзначное число.
52. См. рис. 59. 53. Тем
или иным языком владеют 90 школьников, так как по условию 10 человек не
освоили ни одного языка. Из этих 90 человек 15 не сдали немецкий, так
как 75 его сдали по условию, а 7 человек не сдали английский, так как 83
его сдали по условию. Значит, всего не сдавших один из экзаменов 22
человека (поскольку 15 + 7 = 22).
Двумя языками овладели 68 школьников (90–22 = 68).
54. Любая посуда правильной цилиндрической
формы, если смотреть на нее сбоку, представляет собой прямоугольник. Как
известно, диагональ прямоугольника делит его на две равные части. Точно
так же цилиндр делится пополам эллипсом. Из наполненной водой посуды
цилиндрической формы надо отливать воду до тех пор, пока поверхность
воды с одной стороны не достигнет угла посуды, где ее дно смыкается со
стенкой, а с другой стороны края посуды, через который она выливается. В
этом случае в посуде останется ровно половина воды (рис. 60).
 55. Может
показаться, что за указанный период стрелки часов совпадут всего 3
раза: в 12 часов дня, потом в 24 часа этого же дня и в 12 часов
следующего дня. На самом же деле часовая и минутная стрелки совпадают
каждый час 1 раз (когда минутная обгоняет часовую). С 6 часов утра
одного дня до 10 часов вечера другого дня проходит 40 часов – значит, за
это время часовая и минутная стрелки должны совпасть 40 раз. Но 3 часа
из этих 40 часов составляют исключение: это 12 часов одного дня, 24 часа
того же дня и 12 часов другого дня. Представим себе, что в 12 часов
стрелки совпали, в следующий раз минутная стрелка догонит часовую не в
первом часу, а в начале второго, т. е. с 12 часов до 1 часа (неважно –
дня или ночи) совпадения стрелок не происходит. Следовательно, часовая и
минутная стрелки с 6 часов утра одного дня до 10 часов вечера другого
дня совпадут 37 раз.
56. Скорость теплохода примем за х, а скорость реки за у. Поскольку
от Нижнего Новгорода до Астрахани теплоход плывет по течению, то его
собственная скорость и скорость реки складываются, т. е. до Астрахани он
плывет со скоростью (х + у). На обратном пути теплоход плывет против течения, т. е. со скоростью (х – у).
Как известно, расстояние равно произведению скорости на время. Зная,
что теплоход проделывал один и тот же путь за 5 и за 7 суток, можно
составить уравнение:
5(х + у) = 7(х – у).
Преобразуем его:
5х + 5у = 7х – 7у,
7у + 5у = 7х – 5х,
12у = 2х,
6у = х.
Как видим, собственная скорость теплохода в 6 раз больше
скорости реки. Значит, по течению (от Нижнего Новгорода до Астрахани)
он плывет со скоростью в 7 раз большей скорости реки, ведь в этом случае
скорости теплохода и реки складываются. Поскольку плот плывет только по
течению, то его скорость равна скорости реки, а значит, она в 7 раз
меньше, чем скорость теплохода на пути в Астрахань. Следовательно, и
времени на тот же путь плот затратит в 7 раз больше, чем теплоход:
5 · 7 = 35.
Расстояние от Нижнего Новгорода до Астрахани плот пройдет за 35 суток.
57. Можно с ходу ответить, что 12 куриц за 12
дней снесут 12 яиц. Однако это не так. Если три курицы за три дня несут
три яйца, значит, одна курица за те же три дня несет одно яйцо.
Следовательно, за 12 дней она снесет 12: 3 = 4 яйца. Если же куриц будет
12, то за 12 дней они снесут 12 · 4 = 48 яиц.
58. 111 – 11 = 100.
59. Конечно же, это рассуждение неверно.
Видимость его правильности и убедительности создается за счет того, что в
нем почти незаметно смешиваются и подменяются понятия «сутки» и «день»,
а вернее – «рабочий день». А это совершенно разные понятия, ведь сутки –
это 24 часа, а рабочий день – это 8 часов. В году 365 суток, и это то
время, в которое мы и работаем, и отдыхаем, и спим. В рассуждении же
понятие «365 суток» подменяется понятием «365 дней», и предполагается,
что все эти дни (а на самом деле – сутки) заняты только работой. Далее
из этих «365 дней» вычитается время, затрачиваемое на сон, на отдых и
т. д., а это время надо вычитать не из дней (причем рабочих дней), а из
суток. Тогда количество дней (рабочих) останется прежним, и
недоразумения не возникнет.
60. Надо взять второй наполненный стакан
слева и перелить его во второй пустой стакан справа, тогда наполненные и
пустые стаканы будут чередоваться (рис. 61). 61. Рассуждение
неверно. Говорить о том, что большее количество рабочих сможет
построить дом намного быстрее, можно только в пределах целых дней, т. е.
если измерять время работы днями. Если же измерять это время часами, а
тем более минутами и секундами, то данная закономерность (больше рабочих
– быстрее работа) не действует. Ошибка рассуждения заключается в том,
что в нем смешиваются различные понятия, обозначающие разные временные
интервалы. Понятие «день» почти незаметно подменяется понятиями «час»,
«минута», «секунда», за счет чего и создается видимость правильности
данного рассуждения.
62. Это слово «неправильно». Оно всегда так и
пишется – «неправильно». Эффект этой задачи-шутки заключается в том,
что в ней слово «неправильно» употребляется в двух разных смыслах.
63. Попугай действительно может повторять каждое услышанное слово, но он глух и не слышит ни одного слова.
64. Конечно же, спичку, так как без нее
нельзя зажечь ни свечу, ни керосиновую лампу. Вопрос задачи
двусмысленен, ведь его можно понимать то ли как выбор между свечой и
керосиновой лампой, то ли как последовательность в зажигании чего-либо
(сначала спичка, а уж от нее – все остальное).
65. Может показаться, что Петр будет спать 14
часов, но на самом деле он сможет поспать всего 2 часа, потому что
будильник прозвонит в 9 часов вечера. Простой механический будильник не
различает дня и ночи и всегда звонит в то время, на которое его
поставили. Если бы это был электронный будильник компьютерного типа,
который можно программировать, тогда Петру удалось бы проспать с 7 часов
вечера до 9 часов утра.
66. Логическая закономерность, что отрицание
истины является ложью, а отрицание лжи – истиной, действует только
тогда, когда речь идет об одном и том же предмете. В данном случае речь
должна идти об одном и том же предложении. Если бы это было так, то одно
утверждение обязательно было бы истинным, а другое ложным, или
наоборот. Но в задаче речь идет о двух разных предложениях. Поэтому нет
ничего удивительного в том, что они оба являются ложными.
67. Сумма восьми цифр, равная двум, может
получиться в том случае, если одна из этих цифр – двойка, а остальные –
нули. Такое восьмизначное число только одно. Это 20 000 000. Но сумма
восьми цифр, равная двум, также может получиться в том случае, если две
из этих цифр единицы, а остальные нули. Таких восьмизначных чисел семь:
11 000 000, 10 100 000, 10 010 000, 10 001 000, 10 000 100, 10 000 010,
10 000 001.
Итак, существует восемь восьмизначных чисел, сумма цифр которых равна двум.
68. Периметр фигуры – это сумма длин всех ее
сторон. В данной фигуре 12 сторон. Если ее периметр равен 6, то одна
сторона равна 6: 12 = 0,5. Фигура состоит из 5 одинаковых квадратов, со
стороной 0,5.
Площадь одного квадрата равна 0,5 · 0,5 = 0,25. Следовательно, площадь всей фигуры равна 0,25 · 5 = 1,25.
69. Затруднение при решении может возникнуть
из-за необычно сформулированного условия задачи. Сама же задача очень
проста. Требуется всего лишь записать математически то, что выражено в
ней словами, т. е. распутать ее словесное условие. Сумма квадратов чисел
2 и 3 – это 22 + 32. Куб суммы квадратов чисел 2 и 3 – это (22 + 32)3. Сумма кубов этих чисел – это 23 + 33. Квадрат этой суммы – это (23 + 33)2. Надо найти разность первого и второго:
(22 + З2)3 – (23 + З3)2 = (4 + 9)3 – (8 + 27)2 = 133 – 352 = 2197–1225 = 972.
70. Это число 2. Половина этого числа равна 1, а половина от половины этого числа (т. е. единицы) равна 0,5, т. е. тоже половине.
71. Рассуждение неверно. Совершено не
обязательно, что Саша Иванов со временем побывает на Марсе. Внешняя
правильность этого рассуждения создается за счет употребления в нем
одного слова человек в двух разных смыслах: в широком (абстрактный представитель человечества) и в узком (конкретный, данный, именно этот человек).
72. Как видим по условию, для получения
оранжевой краски требуется в 3 раза больше желтой краски, чем красной:
6: 2 = 3. Значит, из имеющегося количества желтой и красной красок надо
взять в 3 раза больше желтой краски, чем красной, т. е. 3 грамма желтой и
1 грамм красной. Можно получить 4 грамма оранжевой краски.
73. См. рис. 62. Можно убрать и другие 2 спички.
74. Надо поставить запятую: 5 < 5, 6 < 6.
75. Сначала надо выяснить, каков общий возраст всех игроков команды: 22 · 11 = 242. Возраст выбывшего игрока примем за х. После того как он выбыл, общий возраст игроков команды стал равен 242 – х. Поскольку игроков стало 10 и их средний возраст известен (21 год), можно составить следующее уравнение:
(242 – х): 10 = 21,
242 – х = 210,
х = 242–210 = 32.
Выбывшему игроку 32 года.
76. Рассуждение, конечно же, неверно. Эффект
его внешней правильности достигается благодаря употреблению понятия
«возраст отца» в двух разных смыслах: возраст отца как возраст человека,
который является этим отцом, и возраст отца как число лет отцовства.
Кстати, во втором значении понятие возраст, как правило, не употребляется: обычно под словосочетанием возраст отца понимается возраст этого человека, а не что-либо иное.
77. Сначала надо разделить 24 килограмма
гвоздей на две равные части по 12 килограммов, уравновесив их на чашах
весов. Затем так же разделить 12 килограммов гвоздей на две равные части
по 6 килограммов. После этого отложить одну часть, а другую разделить
таким же способом на части по 3 килограмма. Наконец к шестикилограммовой
части гвоздей добавить эти 3 килограмма. В результате получится 9
килограммов гвоздей.
78. Это был четверг. В этот день Петр
правдиво сказал, что вчера (т. е. в среду) он лгал, а Иван солгал насчет
того, что вчера (т. е. в среду) он лгал, ведь по условию в среду он
говорит правду.
79. Это число 147.
80. 81. В
1001 раз. Для того чтобы установить это, надо шестизначное число,
полученное путем дублирования трехзначного числа, разделить на это
трехзначное число. Получится 1001 (см. также задачу 51).
82. Ошибка данного рассуждения заключается в
утверждении, что если бы не было времени, то не было бы ни одного дня, а
значит, всегда стояла бы ночь. Как раз наоборот – если бы не было
времени, то не могло бы быть ни одного дня и ни одной ночи, ведь понятие
ночи (как и понятие дня) относится именно ко времени (и день, и ночь –
это некие временные интервалы).
83. Примем число яблок, которые взяла Настя из первой корзины, за х, тогда в первой корзине осталось (12 – х) яблок. Именно столько яблок и взяла Маша из второй корзины. Значит, во второй корзине осталось
(12 – (12 – х)) яблок.
В двух корзинах вместе осталось
(12 – х) + 12 – (12 – х) = 12 – х + 12–12 + х = 12.
В двух корзинах вместе осталось 12 яблок.
84. Этого не может сказать ни одна свинья,
ведь свиньи, как известно, не говорят. Эта не очень серьезная задача
основана на двусмысленности вопроса: «Сколько свиней могут сказать…?»
Слово «сказать» в этом вопросе можно понимать буквально – говорить
членораздельной человеческой речью, а также его можно воспринимать в
переносном значении – кто-то говорит от имени или за тех, которые сами
говорить не могут (не умеют).
85. Сапожник и плотник – это одно лицо. В этом легко убедиться, составив простую схему: 86. Рассуждение
неверно. Ошибка заключается в смешивании двух различных ситуаций в
одних и тех же словах. Когда рабочие строят дом, их усилия складываются,
поэтому работа идет быстрее и выполняется за более короткий срок. Когда
корабли пересекают Атлантический океан, то их «усилия» не складываются:
каждый корабль преодолевает океан все равно в одиночку, и поэтому
время, затраченное на переправу через океан, не уменьшается при
увеличении количества кораблей.
87. Стрелка у весов была сдвинута не вправо
от нуля, а влево, т. е. весы показывали на 1 килограмм меньше. Значит,
Петин портфель весит 3 килограмма, а Сашин – 4 килограмма. Вместе их
портфели весят 7 килограммов. Когда мальчики их взвесили, весы показали
на 1 килограмм меньше, т. е. 6 килограммов.
88. На первый взгляд, подобным образом можно
расположить только 9 кружочков, но ведь в условии не сказано, что ряды
кружочков должны быть горизонтальными или вертикальными. Они могут быть
какими угодно. Расположить кружочки можно различными способами
(рис. 63). 89. Может
показаться, что оставшегося куска хватит на семь стирок. Однако это не
так. Если длина, ширина и высота куска мыла уменьшились вдвое, то его
объем уменьшился не в 2 раза, а в 8 раз: Если после семи стирок объем куска мыла уменьшился в 8 раз, значит, оставшегося куска хватит всего на одну стирку (рис. 64). 90. Кусок
материи в 2/3 метра надо сложить пополам. Образовавшаяся линия сгиба
поделит его на две равные части по 1/3 метра. Затем надо сложить его еще
раз пополам. Образовавшиеся линии сгиба поделят кусок материи на четыре
равные части по 1/6 метра. Три таких части – это 3/6 метра, или искомая
1/2 метра (рис. 65). 91. Конечно
же, композитором, равно как и художником, писателем или ученым, надо
родиться, ведь если человек не родится, то он не сможет сочинять музыку,
рисовать картины, писать романы или делать научные открытия. Эта
шуточная задача основана на двусмысленности вопроса: «Действительно ли
надо родиться?» Данный вопрос можно понимать буквально: надо ли
рождаться на свет для того, чтобы заниматься каким-либо видом
деятельности; а также данный вопрос можно понимать в переносном смысле:
является ли талант композитора (художника, писателя, ученого)
врожденным, данным от природы или же он приобретается во время жизни
упорным трудом.
92. Рассуждение, конечно же, неверно. Его
внешняя правильность основана на почти незаметном исключении еще одного
варианта, который в данном рассуждении также необходимо было
рассмотреть. Это вариант, когда не видит ни один глаз. Именно он и был
пропущен: «Без правого глаза мы видим, без левого тоже, значит, глаза не
обязательны для зрения». Правильное утверждение должно быть таким: «Без
правого глаза мы видим, без левого тоже видим, но без двух вместе не
видим, значит, мы видим или одним глазом, или другим, или двумя вместе,
но мы не можем видеть без глаз, которые, таким образом, необходимы для
зрения».
93. На первый взгляд может показаться, что
попугаю можно задать до 99 вопросов. На самом же деле можно обойтись
гораздо меньшим числом вопросов. Спросим его так: «Тебе больше 50 лет?»
Если он ответит «да», то его возраст от 51 до 99 лет; если же он ответит
«нет», то ему от 1 года до 50 лет. Количество вариантов его возраста
после первого же вопроса сокращается вдвое. Следующий подобный вопрос:
«Тебе больше (можно спросить – меньше) 25 лет?», «Тебе больше (меньше)
75 лет?» (в зависимости от ответа на первый вопрос) сокращает число
вариантов в 4 раза и т. д. В итоге попугаю надо задать всего 7 вопросов.
94. Этот рисунок можно видеть по-разному.
Присмотритесь к нему внимательно, и вы заметите, как изображение будет
переворачиваться то в одну, то в другую сторону, как бы переливаться на
ваших глазах. В одном случае мы видим шесть кубиков – три сверху, два
посередине и один снизу, а в другом случае мы видим один кубик – в
середине рисунка. Таким образом, всего на рисунке изображено семь
кубиков.
95. Тереть теленка можно сколь угодно долго,
однако сколько теленка ни три, у него все равно будет четыре ноги. Эта
задача-шутка основана на том, что числительное «три» имеет омоним –
глагол в повелительном наклонении.
96. Рассказчик разделил веревку не поперек,
как, скорее всего, может показаться, а вдоль, сделав из нее две веревки
одинаковой длины. Когда он связал две части вместе, веревка стала в 2
раза длиннее, чем была сначала.
97. При вычитании меньшего числа из большего
действует одна закономерность: сумма всех цифр разности всегда будет
равна 18 (независимо от исходных чисел). Кроме того, второй цифрой
разности всегда будет 9. Таким образом, зная последнюю цифру разности
(или первую), можно безошибочно установить всю разность.
98. Если бы не семеро, а трое пошли, то все равно те же самые семь рублей и нашли.
99. См. рис. 66. 100. На
первый взгляд может показаться, что зазор будет настолько маленьким
(ведь 10 метров – это почти ничто по сравнению с 40 000 километров), что
в него не сможет пролезть не только человек, но даже кошка. На самом же
деле величина зазора будет приблизительно равна 1,6 метра, т. е.
человек не только сможет пролезть в него, но даже пройти (может быть,
слегка наклонив голову).
Как известно, длина окружности равна 2ϖR, где R – ее радиус. Значит, радиус окружности равен L/2ϖ, где L – длина
окружности. Таким образом, длина окружности и ее радиус находятся в
отношении прямой пропорциональности, но при этом радиус меньше длины.
Увеличение длины экваториального обруча – это увеличение
длины окружности. Пользуясь вышеприведенной формулой, легко установить
увеличение ее радиуса, которое будет величиной зазора, образовавшегося
между обручем и поверхностью земного шара. Произведя простые подсчеты,
вы увидите, что при увеличении длины экваториального обруча всего на 1
метр, его радиус увеличивается приблизительно на 16 сантиметров. В такой
зазор может пролезть кошка. Увеличение длины обруча на 10 метров (как в
условии задачи) увеличивает зазор приблизительно на 1,6 метра, и в него
может пройти человек. Если же длина экваториального обруча увеличится
на 100 метров, то величина зазора будет приблизительно равна 16 метрам. В
такой зазор вполне сможет «пролезть» пятиэтажный дом.
|

